nlp-intro2
by 정 찬
저번 nlp-intro 시리즈에서는 자연어 처리가 무엇인지, 벡터(인코딩)를 이용해서 어떻게 자연어처리를 하는지, 통계적 방법론에는 어떤 기법들이 있는지 살펴 봤습니다.
이번, 그리고 다음 포스팅에서 이름도 무시무시한 딥러닝이 NLP에서 어떻게 적용되는지 알아볼 예정입니다.
Index
- 딥러닝deep-learning은 무엇이고, 통계적 방법과 무엇이 다르길래?
- 이론적으로 어떻게 구현할 수 있는지
- word embedding: Glove, Word2Vec
- 차원 축소dimensionality reduction
- 벡터 유사도 구하기: 코사인 유사도cosine similiarity
1. 딥러닝deep-learning은 무엇이고, 통계젹 방법과 무엇이 다르길래?
저번 시간에는 NLP의 기본 개념과 통계적 모델에 대해 배웠습니다. 그리고 통계적 모델의 한계로
- 너무 큰 벡터의 크기
- 단어 유사도를 알 수 없음
- 문맥상 순서가 중요한 글에 적용하기 어려움
이렇게 세가지를 정리했었습니다.
그러면서 말미에 딥러닝을 활용하면 문제를 해결할 수 있다고 했었죠. 먼저 딥러닝deep-learning이 무엇인지, 통계적 모델과 어떻게 다른지 알아봅시다.
1.1. 딥러닝deep-learning
딥러닝을 말 그대로 해석하면 깊이deep + 배운다learning가 됩니다. 누군가는 이렇게 생각하실 수도 있겠네요.
"아니~ 컴퓨터는 0하고 1로 된 숫자만 계산한다면서요~ 어떻게 깊게 배워요! 그래봐야 숫자가 숫자지!!"
저번 시간에 배웠듯이 컴퓨터가 0과 1로 된 벡터로 사고하는 것은 맞는 말입니다. 자 그러면 deep하다는게 무슨 의미일지 알아봅시다.
혹시 저번 **딥러닝을 이용한 자연어 처리-1**의 초반 내용을 보셨는지 모르겠습니다. 신경망에 대해 먼저 간단하게 이해해 봅시다.
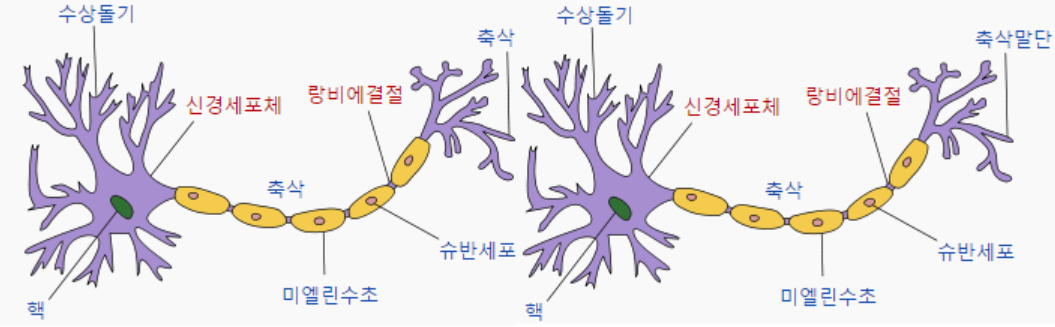
🧠신경망neural network
신경망은 원래 뇌과학에서 사용하는 생물학, 의학적 개념이었습니다. 하나의 뉴런이 다른 뉴런에게 신호를 주고 받는 과정이 신경망이라고 생각하시면 됩니다. 예컨대 의자에 발을 닿았다고 합시다. 약하게 스치듯 닿으면 우리는 아프다고 느끼지는 않습니다. 하지만 세게 부딪히면 아픈 기준치를 넘어서기 때문에 발 끝의 신경에서부터 뇌의 신경까지 통각이 전해지는 것이죠. 무릎 쯤에서 "음.. 이건 소리 지를 만큼 아프지는 않네!"라고 신호를 전달할 수도 있구요.
발가락: 아파 ->
발: 아파 ->
종아리: 아파 ->
...
뇌: 앗, 지금 발가락이 아프구나!
1.2. 인공신경망 artificial neral network🤖🧠
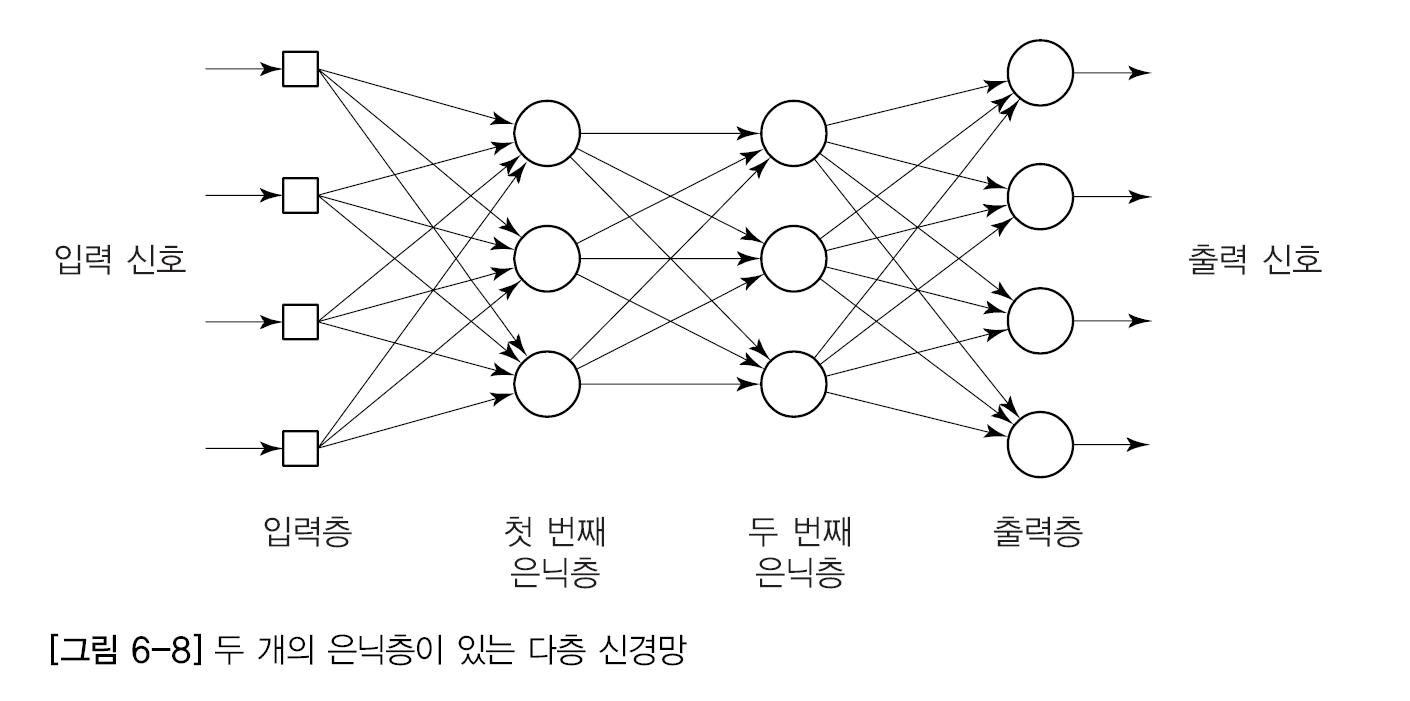
인공신경망은 이러한 생물학적인 뉴런 개념을 수학적으로 모델링 해 만들어졌습니다. 즉, 어떤 임계점을 넘으면 신호를 전달하고, 그렇지 않으면 전달하지 않습니다. (자세한 내용은 딥러닝을 이용한 자연어처리 시리즈에서 추가로 설명하겠습니다.)
그리고 발가락, 발, 종아리, ..., 뇌까지 전달되는 뉴런이 무수히 많았던 것처럼 여러 층을 만들어서 틀릴 가능성을 줄입니다.
그래서.. 딥러닝이 왜 좋은건데요..?
먼저 Language Model에 대해 공부하고 그 한계점을 짚으면서 생각해 봅시다.
1.3. Languge Model(LM)
우리가 말이나 글을 쓸 때 문법을 떠올리면서 조합하지는 않죠. 그냥 "날씨가" 다음에 보통 "좋다", "나쁘다", "해가 날 것 같다" 등 맥락적으로 적당한 단어를 선택합니다. 그렇다면 적합할 확률이 있겠죠?
Language Model은 통계적 모델의 발전된 버전이라고 생각하시면 됩니다.
전체 문장Sentence
모든 문장이 포함된 데이터Data
그 속에 사용된 단어Vocabulary
LM에서는 데이터를 이렇게 세가지로 나눈 다음 문장Sentence이 통계적으로 문맥에 맞는지 판단합니다. 우리는 무수히 많은 문장을 data로 입력해 주면 컴퓨터는 이 단어 뒤에 해당 단어가 많이 오는지, 즉 문맥에 맞는지 판단합니다.
에컨대 전체 corpus에 "날씨가" 다음에 좋다, 나쁘다 같은 문장이 많이 수집되었다고 합시다. 하지만 전체 단어vocabulary 중에 "문어"라는 단어가 있다고 해서 우리가 "날씨가 문어다"🐙라고 말하지는 않습니다. 즉, 전체 문장에서 "날씨가" 다음에 "문어"가 나온적이 없다면 통계상 문맥에 어울리지 않는다고 판단하는 방식입니다. 물론 Smoothing이라는 방식으로 아예 나오지 않은 단어도 0%라고 말하지는 않습니다. smoothing에 대한 자세한 내용은 따로 찾아보시길:)
이거 혹시 어디서 들어본 것 같지 않나요? 네. 지금까지 저번 nlp-intro-1에서 배웠던 N-gram 개념을 활용한 N-gram LM에 대해 이야기 했습니다. 1, 2, 3개의 단어를 같이 고려하면서 맥락을 이해하는 것이죠. 데이터가 크고, 다양할수록 좋은 모델이 됩니다.
😅통계적 모델의 한계
통계적 모델들을 배울 때
- 너무 큰 벡터의 크기
- 단어 유사도를 알 수 없음
- 문맥상 순서가 중요한 글에 적용하기 어려움
이렇게 세가지의 문제가 있었습니다. 하나 더 추가하자면
- vocabulary에 들어가지 못한 단어들이 무시됩니다. (확률이 0에 수렴)
아예 확률의 분모, 분자에 들어가 있지 않기 때문이죠. 수집한 글감에 따라서 정확도가 떨어질 수 있습니다. 즉, 일반화 능력이 떨어집니다.
예컨대 play 뒤에 soccer, basketball, baseball이라는 단어가 오는 글감을 수집했는데 갑자기 play 다음에 floorball이 나오면 컴퓨터는 음.. play 다음에 floorball이 나온적 없으니까 틀렸어!!!라고 정해버립니다. 우리는 그래도 무슨 ball이니까 스포츠라서 play 뒤에 쓸 수 있다고 유추하는데 말입니다.
다른 예로 추리 소설 한 권의 글을 vocabulary로 만들었다고 합시다. 그렇다면 범죄나 법, 사건과 관련된 단어들은 많이 수집되겠지만, 순수 과학에 대한 논문이나 식사를 주문하는 대화 내용에 대한 정확도는 떨어지겠죠? 인터넷 상의 댓글도 잘 해석하지 못할겁니다. 주머니에 들어있지 않은 단어이기 때문에 컴퓨터가 알 방도가 없습니다. 이러한 확장 불가능한 점 또한 통계적 모델의 한계입니다.
1.4. 딥러닝 기반 NLP의 기본! Embedding!
딥러닝이 뭔지도 대강 알겠고..
통계적 모델이 어떤 한계가 있는지도 알겠는데..
그래서 딥러닝은 자연어 처리에 어떻게 사용되나요..?
뭐니뭐니 해도 딥러닝과 NLP가 결합하는 시작점에는 Embedding이 있습니다.
Embed는 원래 깊숙이 박아 넣는다는 의미를 가진 단어입니다. embedded하면 분사형으로 (외부로부터 독립적으로) 내포된 정도의 의미가 되겠군요. 기계 각 부분은 이미 존재하고, 따로 삽입되어 전체적인 제어를 담당하는 embedded system을 생각하시면 이해가 편하실지도 모르겠습니다.
딥러닝에서 Embedding은 희소행렬sparse matrix, 희소 표현sparse representation 문제를 해결하기 위해 적용되었습니다. 희소행렬은 '사과'를 표현하는데 corpus의 단어 수 만큼의 빈 공간(0)이 필요해 연산에 방해가 되었습니다.
예)
corpus 크기: 10,000
사과 = [0, 0, 0, 0, 1, 0, 0, ..., 0]
이때, 1 이후 9995개의 0이 있음..!
그렇다면 이 차원을 줄여서 계산하기 쉽게 만들 수는 없을까요? 그 방법을 Word Embedding이라고 하고, embedding을 통해 도출된 행렬을 밀집표현dense representation, 그러한 벡터를 밀집 벡터dense vector라고 합니다. 희소sparse의 반대말은 밀집dense이기 때문이죠! 이때 행렬의 값은 더이상 0과 1이 아니라 실수 값을 갖게 됩니다.
예)
사과 = [0.12, 2.1, -1.5, 0.3, ...]
이때, 사과 벡터의 차원을 128로 고정시킴 -> 사과 벡터의 길이는 128
아쉬우니까 Embedding에 대해 간단하게 설명하자면(다음 시간에 배웁니다)
word embedding은 각 단어들을 vector로 바꾸어 벡터 공간vector space의 적당한 위치에 배치할 수 있도록 학습
즉, 유사한 단어들이 그래프 위에 가깝게 위치하게 함.
이를 가능하게 하는 수학적 기법은 유사도similarity(보통 코사인 유사도cosine similarity. 드물게 유클리드, 자카드 유사도 사용)
정리하자면
원-핫 벡터와 임베딩 벡터의 차이
| one-hot vector | embedding vector | |
|---|---|---|
| 차원 | 고차원(corpus 크기 만큼) | 저차원(원하는 크기) |
| 다른 표현 | 희소 벡터sparse vector | 밀집 벡터dense vector |
| 표현 방법 | 수동 | 훈련 데이터로부터 학습 |
| 값의 타입 | 0, 1 | 실수real number |
Em
이렇습니다.
마치며
다음 포스팅에서 Embedding이 가능하도록 만든 차원 축소 기술들(PCA, SVD, LDA)의 기본 개념을 간단하게 설명하고, 대표적인 Word Embedding 기법인 LSA, Word2Vec, FastText, Glove 등에 대해 살펴보겠습니다.
차원 축소에 대한 자세한 내용은 딥러닝을 이용한 자연어 처리시리즈에서 차차 설명해 드리겠습니다.
최대한 쉽게 작성하느라 넘겨버린 부분이 있을지도 모르겠네요. 혹시 이론적으로 부족하거나 논리적 비약으로 느껴지신다면 jung666597@cosadama.com으로 연락 부탁드립니다.🙏
그럼, 다음 포스팅에서 만나요~
참고자료
딥러닝을 이용한 자연어 처리 입문 part1-3, 5, 10
jiho-ml Weekly NLP 4,5,6,7,9,10,11,12,13,14,17