Machine Learning(Harvard) Classification study
by 나다경
Classification
분류는 모집단의 표본이 속하는 작은 클래스 집합을 예측하려고 한다. 수학적으로, 그 목적은 특징 벡터 $x$를 아는 것에 기반을 둔 레이블인 $y$를 찾는 것이다. 예를 들어, 사람의 얼굴을 보는 것으로부터 성별을 예측하는 것을 고려해 보자. 기계가 이것을 잘하게 하기 위해서, 우리는 일반적으로 기계에 '남성' 또는 '여성'으로 분류된 사람들의 이미지들을 공급하고 이미지 속의 사람의 성별을 배우게 할 것이다. 그런 다음, 새로운 사진이 주어지면, 학습된 알고리즘은 사진 속 인물의 성별을 우리에게 돌려준다.
분류에는 여러 가지 방법이 있다. 한 아이디어는 아래 이미지에서 도식적으로 보여지며, 여기서 우리는 2차원 형상 공간에서 두 가지 다른 유형의 '물건'을 나누는 선을 찾는다.
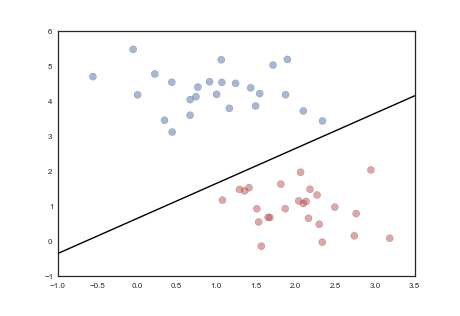
%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")
from PIL import Image
c0=sns.color_palette()[0]
c1=sns.color_palette()[1]
c2=sns.color_palette()[2]
from matplotlib.colors import ListedColormap
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
def points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=True, colorscale=cmap_light, cdiscrete=cmap_bold, alpha=0.1, psize=10, zfunc=False, predicted=False):
h = .02
X=np.concatenate((Xtr, Xte))
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
#plt.figure(figsize=(10,6))
if zfunc:
p0 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 0]
p1 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z=zfunc(p0, p1)
else:
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
ZZ = Z.reshape(xx.shape)
if mesh:
plt.pcolormesh(xx, yy, ZZ, cmap=cmap_light, alpha=alpha, axes=ax)
if predicted:
showtr = clf.predict(Xtr)
showte = clf.predict(Xte)
else:
showtr = ytr
showte = yte
ax.scatter(Xtr[:, 0], Xtr[:, 1], c=showtr-1, cmap=cmap_bold, s=psize, alpha=alpha,edgecolor="k")
# and testing points
ax.scatter(Xte[:, 0], Xte[:, 1], c=showte-1, cmap=cmap_bold, alpha=alpha, marker="s", s=psize+10)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
return ax,xx,yy
def points_plot_prob(ax, Xtr, Xte, ytr, yte, clf, colorscale=cmap_light, cdiscrete=cmap_bold, ccolor=cm, psize=10, alpha=0.1):
ax,xx,yy = points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=False, colorscale=colorscale, cdiscrete=cdiscrete, psize=psize, alpha=alpha, predicted=True)
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=ccolor, alpha=.2, axes=ax)
cs2 = plt.contour(xx, yy, Z, cmap=ccolor, alpha=.6, axes=ax)
plt.clabel(cs2, fmt = '%2.1f', colors = 'k', fontsize=14, axes=ax)
return ax
Using sklearn : The heights and weights example
우리는 분류기에 대한 이해를 향상시키기 위해 남성과 여성의 키와 무게의 데이터 세트를 사용할 것이다. 우리는 데이터를 데이터 프레임에 로드하고 그림을 그릴 것이다.
dflog = pd.read_csv("data/01_heights_weights_genders.csv")
dflog.head()
우리가 항상 사용할 데이터의 형태는

'응답'을 일반 배열로 하여
[1,1,0,0,0,1,0,1,0....]
plt.figure(figsize=(20,15))
plt.scatter(dflog.Weight, dflog.Height, c=[cm_bright.colors[i] for i in dflog.Gender == 'Male'], alpha=0.08);

from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
def cv_score(clf, x, y, score_func = accuracy_score):
result = 0
nfold = 5
# split data into train/test groups, 5 times
for train, test in KFold(y.size, nfold):
# fit
clf.fit(x[train], y[train])
# evaluate score function on held-out data
result += score_func(clf.predict(x[test]), y[test])
# average
return result / nfold
from sklearn.model_selection import train_test_split
Xlr, Xtestlr, ylr, ytestlr = train_test_split(dflog[['Height','Weight']].values, (dflog.Gender=="Male").values)
#the grid of parameters to search over
Cs = [0.001, 0.1, 1, 10, 100]
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_validate, cross_val_score
max_score = 0
for C in Cs:
clf = LogisticRegression(C=C)
score = cross_val_score(clf, Xlr, ylr,cv=5)
max_score = 0.932
best_C = 0.1
print(max_score, best_C) #0.932 0.1
clfl = LogisticRegression(C=best_C)
clfl.fit(Xlr, ylr)
ypred = clf1.predict(Xtestlr)
accuracy_score(ypred, ytestlr) #0.9212
from sklearn.model_selection import GridSearchCV
clfl2 = LogisticRegression()
parameters = {'C': [0.0001, 0.001, 0.1, 1, 10, 100]}
fitmodel = GridSearchCV(clfl2, param_grid=parameters, cv=5, scoring='accuracy')
fitmodel.fit(Xlr, ylr)
fitmodel.best_estimator_, fitmodel.best_params_, fitmodel.best_score_, fitmodel.cv_results_ #'C': 0.1
clfl2 = LogisticRegression(C=fitmodel.best_params_['C'])
clfl2.fit(Xlr, ylr)
ypred2 = clfl2.predict(Xtestlr)
accuracy_score(ypred2, ytestlr) #0.9212
How to Classify
앞에서 회귀 분석을 수행하기 위해 경험적 위험 최소화(ERM)과 함께 제곱 오류 손실 함수를 사용했다. 그 아이디어는 훈련 세트에 대한 이러한 위험을 계산하고 최소화하는 것이었다. 그 결과 모집단 또는 표본 외 위험의 크기가 표본 내 훈련 위험과 비슷하여 크기가 작을 것으로 기대되었다.
분류에 적합한 위험은 무엇일까? 하나는 잘못 분류된 검체의 비율이다.
이는 각 표본에 대해 1-0 손실을 선택하는 것과 같다 :
$$l = \mathbf{1}_{h \ne y}.$$
여기서 $h$는 우리가 내리는 분류 결정이다.(회귀에 대해서는 $l = (h-y)^2$를 사용) 기호 $\mathbf{1}$은 $h$가 점 $y$의 '참' 값과 같지 않을 경우 1로 처벌한다는 것을 의미한다. 그렇다면 위험은 다음과 같다 :
$$ R_{\cal{D}}(h(x)) = \frac{1}{N} \sum_{y_i \in \cal{D}} l = \frac{1}{N} \sum_{y_i \in \cal{D}} \mathbf{1}_{h \ne y_i} $$
따라서 표본 50개 중 5개가 잘못 분류된 경우 위험은 0.1이다. 이는 물론 표본의 90%가 정확하게 분류되었다는 것을 의미한다. 이 숫자를 정확도 점수 또는 유틸리티라고 한다 :
$$ U_{\cal{D}}(h(x)) = \frac{1}{N} \sum_{y_i \in \cal{D}} \mathbf{1}_{h = y_i} $$
The ATM Camera example
당신이 달러 지폐와 수표를 구별할 수 있는 스마트 ATM 카메라를 만드는 일을 맡고 있다고 상상해보라. 달러는 수표로 분류되지 않으며 수표는 달러로 분류되지 않는다.
87개의 수표 및 달러 이미지 세트가 제공되며, 각 이미지 크기는 322 X 137 픽셀로 조정되었으며 각 픽셀에는 3가지 색상 채널이 있다.
data = np.load("data/imag.pix.npy")
y = np.load("data/imag.lbl.npy")
# standardized pixels in image
STANDARD_SIZE = (322,137)
data.shape, y.shape #((87,132342),(87,))
def get_image(mat):
size = STANDARD_SIZE[0]*STANDARD_SIZE[1]*3
r,g,b = mat[0:size:3], mat[1:size:3],mat[2:size:3]
rgbArray = np.zeros((STANDARD_SIZE[1],STANDARD_SIZE[0], 3), 'uint8')#3 channels
rgbArray[..., 0] = r.reshape((STANDARD_SIZE[1], STANDARD_SIZE[0]))
rgbArray[..., 1] = b.reshape((STANDARD_SIZE[1], STANDARD_SIZE[0]))
rgbArray[..., 2] = g.reshape((STANDARD_SIZE[1], STANDARD_SIZE[0]))
return rgbArray
def display_image(mat):
with sns.axes_style("white"):
plt.imshow(get_image(mat))
plt.xticks([])
plt.yticks([])
display_image(data[5])

display_image(data[50])

수표와 달러를 구별하는 데 도움이 될 이 이미지들의 몇 가지 측면은 무엇이라고 생각하는가?
The curse of dimensionality : Feature engineering
가장 먼저 알아챈 것은 많은 특징들을 가지고 있다는 것이다 : 정확히 말하면, $322 x 137 x 3 = 136452$이다. 기능이 너무 많으면 과적합으로 이어질 수 있다.
다항식 회귀 분석 과정에서 우리는 정규화가 다항식에서 계수를 0에 매우 가깝게 함으로써 이러한 능력들 중 일부를 제거하려고 하는 것을 보았다. 그래서 우리가 가진 특징의 수를 줄였다.
이 문제를 해결하는 또 다른 방법은 다음과 같다. 85개의 데이터 지점이 있지만 136452개의 기능이 있다. 즉, 데이터 지점보다 훨씬 많은 기능이 있다. 따라서 몇 가지 속성이 순전히 우연의 일치로 $y$와 상관관계가 있을 가능성이 높다. (이미지가 많거나 '빅데이터'가 과적합에 도움이 된다.)
우리는 여기의 정규화된 회귀에서 일어났던 것과 비슷한 것을 할 필요가 있다. 우리는 문제의 차원을 줄일 수 있는 몇 가지 사전 기능 선택에 참여할 것이다. 여기서 사용할 아이디어는 주성분 분석(PCA) 이다.
PCA는 비지도 학습 기법이다. PCA의 기본 개념은 형상 공간의 좌표 축을 회전시키는 것이다. 우리는 먼저 데이터가 가장 많이 변화하는 방향을 찾는다. 이 방향을 따라 하나의 좌표 축을 설정했는데, 이것을 첫 번째 주성분이라고 한다. 그런 다음 데이터가 두 번째로 많이 변하는 수직 방향을 찾는다. 이것은 두 번째 주성분이다. 이 다이어그램은 이 프로세스를 보여준다. 형상 치수만큼 많은 주성분이 있다. 우리가 수행한 모든 것은 회전이다.
그러면 어떻게 기능을 선택할 수 있을까? 변동 분계점을 결정한다. 특정 방향의 변동이 특정 숫자 아래로 떨어지면 주성분 뒤의 모든 좌표 축을 제거한다. 예를 들어, 세 번째 축 이후 변동이 10% 이하로 떨어지고 10%가 허용 가능한 컷오프라고 결정하면, 우리는 네 번째 차원부터 모든 치수를 제거한다. 즉, 우리는 고차원 문제를 3차원 부분 공간에 투영했다.
차원을 136452에서 60으로 줄이겠다. 우리는 60을 apriori 숫자로 선택한다 : 우리는 그때까지 데이터의 변동이 합리적인 임계값 아래로 떨어질지 알 수 없다. 원래 87행 X 136452열의 치수 데이터를 취하여 87 X 90 데이터 행렬 X로 변환하는 sklearn API에 fit_transform을 사용한다.
from sklearn.decomposition import PCA
pca = PCA(n_components=60)
X = pca.fit_transform(data)
print(pca.explained_variance_ratio_.sum()) #0.9423360639605542
설명되는 분산 비율 pca.explained_variance_ratio_은 형상의 변동이 이 60개의 형상에 의해 설명되는 정도를 알려준다. 특징들을 종합해 보면 94%가 설명된다. 즉, 136452차원에서 60차원 공간으로 내려갈 수 있을 만큼 좋다.
pca.explained_variance_ratio_*100
첫 번째 차원은 변동의 35%, 두 번째 차원은 6%를 차지하며, 차원은 서서히 내려간다.
pc1,pc2...,pc60으로 표시된 60가지 기능과 샘플의 레이블을 사용하여 데이터 프레임을 생성해 보자 :
df = pd.DataFrame({"y":y, "label":np.where(y==1, 'check', 'dollar')})
for i in range(pca.explained_variance_ratio_.shape[0]):
df['pc%i' % (i+1)] = X[:,i]
df.head()
이러한 주 구성 요소의 모양을 살펴보겠다 :
def normit(a):
a=(a - a.min())/(a.max() -a.min())
a=a*256
return np.round(a)
def getNC(pc, j):
size=322*137*3
r=pc.components_[j][0:size:3]
g=pc.components_[j][1:size:3]
b=pc.components_[j][2:size:3]
r=normit(r)
g=normit(g)
b=normit(b)
return r,g,b
def display_component(pc, j):
r,g,b = getNC(pc,j)
rgbArray = np.zeros((137,322,3), 'uint8')
rgbArray[..., 0] = r.reshape(137,322)
rgbArray[..., 1] = g.reshape(137,322)
rgbArray[..., 2] = b.reshape(137,322)
plt.imshow(rgbArray)
plt.xticks([])
plt.yticks([])
display_component(pca,0)

display_component(pca,1)

우리는 처음 두 개의 주요 구성 요소를 취해서 아래 도표에서 수표와 달러를 분리하기에 충분하다는 것을 즉시 알아차린다. 실제로 첫 번째 구성 요소 자체만으로도 충분해 보인다. 우리는 첫 번째 구성요소의 이미지를 보고 달러 중간에 있는 메달이 아마도 이것에 기여했을 것이라고 추측할 수 있다.
plt.figure(figsize=(20,15))
colors = [c0, c2]
for label, color in zip(df['label'].unique(), colors):
mask = df['label'] == label
plt.scatter(df[mask]['pc1'], df[mask]['pc2'], c=color, label=label)
plt.legend()

PCA가 비지도 학습이기 때문에 우리는 기능 변동의 94%를 설명하기 위해 60개의 구성 요소를 사용해야 했지만, 달러와 수표를 구분하기 위해서는 1~2개의 구성 요소만을 사용했다. 우리가 설명하는 유일한 변화는 136452차원 형상 공간의 변화이다. 우리는 $y$ 또는 라벨의 변동을 설명하고 있지 않고 있으며, 이 경우에서와 같이 $y$의 추가 정보로 분류에 필요한 차원이 훨씬 더 낮다는 것이 밝혀질 수 있다.
따라서 분류기를 만들기 위해 처음 몇 개의 주성분만 선택할 수 있다. 본 실습에서는 두 가지 구성 요소를 쉽게 시각화할 수 있으므로, PC1 및 PC2차원의 2차원 분류기를 학습할 것이다.
Classifying in a reduced feature space with kNN
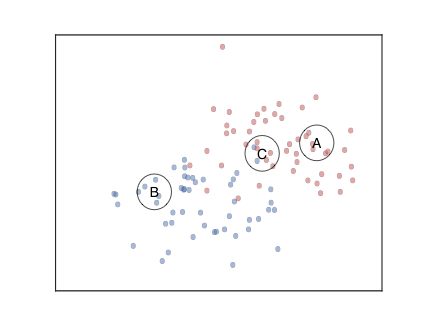
분류 개념에 내포된 것은 형상 공간에서 서로 가까운 표본이 라벨을 공유한다는 개념이다.kNN은 분류를 위한 매우 간단한 알고리즘이다. 기본 개념은 다음과 같다. 형상 공간의 일부 영역에 있는 많은 샘플이 다른 영역에 비해 한 클래스에 속하는 경우 형상 공간의 해당 부분에 해당 클래스에 'belong'으로 레이블을 지정한다. 그런 다음 이 프로세스는 형상 공간을 클래스 기반 영역으로 분류한다. 그런 다음 형상 공간의 점을 고려할 때, 우리는 그것의 내부와 그에 따른 등급을 찾는다.
kNN이 이렇게 하는 방법은 새 샘플의 교육 세트에서 k개의 가장 가까운 이웃을 찾는 것이다. 이 질문에 답하려면 형상 공간에 거리를 정의해야 한다. 이 거리는 일반적으로 유클리드 거리로 정의되며, 이는 두 표본 사이의 각 형상값 차이의 제곱합이다.
$$D(s_1,s_2) = \sum_f (x_{f1} - x_{f2})^2.$$
일단 거리 측정값을 얻으면 현재 샘플과의 거리를 정렬할 수 있다. 그런 다음 우리는 훈련 집합에서 가장 가까운 $k$개를 선택한다. 여기서 $k$는 1,3,5,...19와 같은 홀수이다. 이제 우리는 $k$개의 '가장 가까운 이웃들' 중 얼마나 많은 수가 한 클래스에 속하는지 보고, 그 이웃들 중 다수 클래스를 표본의 클래스로 선택한다.
따라서 훈련 프로세스는 단순히 데이터를 암기하는 것으로 구성되며, 특징 공간의 모든 지점에 있는 $k$개의 가장 가까운 훈련 세트 이웃의 빠른 조회를 돕기 위해 데이터베이스를 사용할 수 있다. 이 프로세스는 특징 공간을 한 클래스 또는 다른 클래스의 영역으로 나눈다. 훈련 세트에서 가장 가까운 $k$개의 이웃이 특징 공간의 주어진 점에 대해 간단히 물어볼 수 있기 때문이다. 또한 분류는 다수 '투표' 방식을 통해 이루어지기 때문에, 형상 공간의 한 점이 원하는 클래스의 해당 점에 가장 가까운 이웃의 비율에 의해 추정된 대로 클래스에 속할 확률도 알고 있다.
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
ys = df['y'].astype(int).values
subdf = df[['pc1', 'pc2']]
subdfstd = (subdf - subdf.mean()) / subdf.std()
Xs = subdfstd.values
def classify(X, y, nbrs, plotit=True, train_size=0.6):
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, train_size=train_size)
clf = KNeighborsClassifier(nbrs)
clf = clf.fit(Xtrain, ytrain)
#in sklearn accuracy can be found by using "score". It predicts and then gets the accuracy
training_accuracy = clf.score(Xtrain, ytrain)
test_accuracy = clf.score(Xtest, ytest)
Xall = np.concatenate((Xtrain, Xtest))
if plotit:
print("Accuracy on training data: %0.2f" % (training_accuracy))
print("Accuracy on test data: %0.2f" % (test_accuracy))
plt.figure()
ax=plt.gca()
points_plot(ax, Xtrain, Xtest, ytrain, ytest, clf, alpha=0.3, psize=20)
return nbrs, training_accuracy, test_accuracy
$k=1$을 선택하면 어떻게 되는지 살펴보자. 교육 세트에서 1NN 분류기는 교육 데이터를 암기한다. 그것은 훈련 세트에서 완벽하게 예측될 것이며, 특히 한 클래스 또는 다른 클래스가 지배하는 특징 공간의 깊은 곳에서 시험 세트는 너무 나쁘게 하지 않을 것이다. 왜냐하면 그 지역에서는 이웃 한 명만 있으면 충분할 수도 있기 때문이다. 그러나 클래스를 확실히 결정하려면 둘 이상의 인접 그룹이 필요하기 때문에 동일한 분류자가 테스트 세트의 분류 경계 근처에서 제대로 작동하지 않는다.
그 결과, 예상할 수 있듯이, 한쪽 또는 다른 쪽으로 분류된 특징 공간의 영역(파란색은 수표, 빨간색은 달러)은 상당히 들쭉날쭉하고 얼룩덜룩하다.
classify(Xs,ys,1)
#Accuracy on training data: 1.00
#Accuracy on test data: 0.91

만약 우리가 50과 같은 $k$에 너무 큰 숫자를 선택한다면, 우리는 우리의 원래 표본으로부터 너무 멀리 방황하는 것이고, 따라서 우리는 많은 양의 형상 공간을 평균한다. 이는 샘플의 위치에 따라 매우 편향된 분류로 이어지지만, 샘플의 위치와는 거리가 멀다. 우리의 분류는 심지어 전체 특징 공간을 포함할 수도 있고, 그 다음에 우리에게 다수 등급을 줄 수도 있다.
확률 측면에서 이러한 부적합 사례는 기준 속도 분류기를 제공한다. $k=N$을 상상해 보자. 그런 다음 확률은 주어진 클래스의 훈련 집합 예제 중 일부일 뿐이다. 파란색 클래스에 대해 이 숫자를 0.4라고 말한다.(즉, 교육 세트에 불균등한 클래스 멤버십이 있는 경우). 이제 임의의 테스트 세트에서 '모두 빨간색으로 분류'라는 분류기를 사용하면 테스트 세트와 훈련 세트가 표본 모집단을 대표하는 경우 평균 60%가 정확할 것이다.
classify(Xs,ys,50)
#Accuracy on training data: 0.60
#Accuracy on test data: 0.57

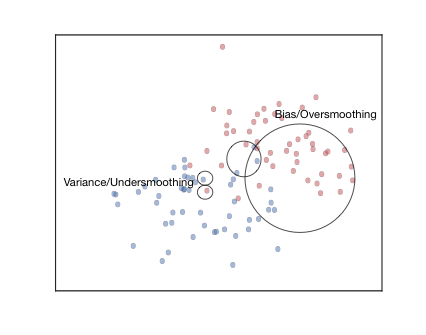
이러한 과적합 및 과소적합 개념은 위의 이미지에 설명되어 있다. 작은 원은 작은 $k$ 근방을 나타내고 큰 원은 큰 $k$ 근방을 나타낸다. 이 원의 왼쪽 아랫부분은 시각적으로 사물의 파란색으로 보일지라도 빨간색으로 분류될 수 있다.
중간 크기의 원은 합리적인 $k$가 무엇을 할 수 있는지 보여준다. 또한 kNN은 분류 경계에서 멀리 떨어져 상당히 안정적이지만 분류 경계 근처에서 더 들쭉날쭉할 가능성이 있다. $k$에 대한 합당한 숫자를 가지면 지글지글한 가장자리가 '매끄러워진다'.
따라서 우리는 다시 한 번 높은 편향(큰 $k$) 사례와 높은 분산 (낮은 $k$)사례 사이의 균형을 찾아야 하며, 적절한 $k$를 찾기 위해 다시 한 번 오차 대 복잡성 곡선으로 눈을 돌린다.
Error against complexity (k), and cross-validation
fits={}
for k in np.arange(1,45,1):
fits[k]=[]
for i in range(200):
fits[k].append(classify(Xs, ys,k, False))
nbrs=np.arange(1,45,1)
fmeanstr = np.array([1.-np.mean([t[1] for t in fits[e]]) for e in nbrs])
fmeanste = np.array([1.-np.mean([t[2] for t in fits[e]]) for e in nbrs])
fstdsstr = np.array([np.std([t[1] for t in fits[e]]) for e in nbrs])
fstdsste = np.array([np.std([t[2] for t in fits[e]]) for e in nbrs])
plt.figure(figsize=(20,15))
plt.gca().invert_xaxis()
plt.plot(nbrs, fmeanstr, color=c0, label="training");
plt.fill_between(nbrs, fmeanstr - fstdsstr, fmeanstr+fstdsstr, color=c0, alpha=0.3)
plt.plot(nbrs, fmeanste, color=c1, label="testing");
plt.fill_between(nbrs, fmeanste - fstdsste, fmeanste+fstdsste, color=c1, alpha=0.5)
plt.legend();

다시 한 번 이전과 같이 이웃 $k$의 수에 대한 검정 오류와 훈련 오류를 표시한다. 여기서 $k$는 이웃의 분류에서 작은 $k$는 더 '흔들림'이고 큰 $k$는 분류를 지나치게 과장하는 복잡도 매개변수의 역할을 한다. x축에 $k$를 거꾸로 표시하여 낮은 복잡도에서 높은 복잡도로 이동한다. 예상대로 교육 오류는 복잡성과 함께 감소하지만 테스트 오류는 다시 올라가기 시작한다. 25에서 5까지 다양한 범위의 $k$가 있으며, 이 경우 적합도는 최고이다.
Setting up some code
교차 검증을 사용하여 분류를 위한 코드를 설정하여 scikit-learn에서 분류 모델을 쉽게 실행할 수 있도록 하자. 먼저 사전 매개 변수로 구현된 분류기 clf, 초 매개 변수 그리드(예:마지막과 같은 복잡성 매개 변수 또는 정규화 매개 변수), Xtrain(샘플 x 특징 배열) 및 ytrain 레이블 세트를 사용하는 함수 cv_optimization을 설정한다. 코드는 트레이닝 세트를 가져다가 n_folds로 분할하고 접힘을 설정하고 각 folds에 대한 훈련 및 유효성 검사 섹션으로 훈련 세트를 분할하여 교차 검증을 수행한다. 매개 변수의 최적 값을 인쇄하고 최상의 분류기를 다시 입력한다.
def cv_optimize(clf, parameters, Xtrain, ytrain, n_folds=5):
gs = GridSearchCV(clf, param_grid = parameters, cv=n_folds)
gs.fit(Xtrain, ytrain)
print('BEST PARAMS', gs.best_params_)
best = gs.best_estimator_
return best
그런 다음 이 최상 분류기를 사용하여 전체 교육 세트에 맞춘다. 이 작업은 do_classify 함수 안에서 수행되며, dataframe indf를 입력으로 사용한다. 목록 형상명의 열을 분류기를 훈련시키는 데 사용되는 형상으로 사용한다. 열 대상 이름은 대상으로 설정한다. 분류는 대상 이름에 target1val 값이 있는 샘플을 값 1로 설정하고 나머지 모든 샘플을 0으로 설정하여 수행된다. 데이터 프레임을 80% 교육 및 20% 테스트로 분할하여 원하는 경우 데이터 세트를 표준화한다. (데이터 세트를 표준화하려면 평균이 0이고 표준 편차의 단위로 설명되도록 데이터 크기를 조정하는 작업이 포함된다.) 그런 다음 교차 검증을 사용하여 교육 세트에서 모델을 교육한다. cv_optimize를 사용하여 최고의 분류기를 얻은 후, 우리는 전체 훈련 세트에 대해 재교육하고 인쇄하는 훈련 및 테스트 정확도를 계산한다. 분할 데이터와 훈련된 분류기를 반환한다.
from sklearn.model_selection import train_test_split
def do_classify(clf, parameters, indf, featurenames, targetname, target1val, standardize=False, train_size=0.8):
subdf = indf[featurenames]
if standardize:
subdfstd = (subdf - subdf.mean()) / subdf.std()
else:
subdfstd = subdf
X = subdfstd.values
y = (indf[targetname].values == target1val)*1
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, train_size = train_size)
clf = cv_optimize(clf, parameters, Xtrain, ytrain)
clf = clf.fit(Xtrain, ytrain)
training_accuracy = clf.score(Xtrain, ytrain)
test_accuracy = clf.score(Xtest, ytest)
print("Accuracy on training data: %0.2f" % (training_accuracy))
print("Accuracy on test data: %0.2f" % (test_accuracy))
return clf, Xtrain, ytrain, Xtest, ytest
As before, cross-validation
지금까지 해왔던 것을 반복하고 교차 검증을 실시한다. 물론 지금은 훨씬 더 작은 집합으로 교육을 받고 있기 때문에 위의 다이어그램과는 결과가 약간 다를 것이다. 우리는 그 결과를 아래 도표에 표시했다. 결과는 상당히 안정적이며 첫 번째 주성분이 기본적으로 데이터를 분리한다는 직관과 일치한다.
bestcv, Xtrain, ytrain, Xtest, ytest = do_classify(KNeighborsClassifier(), {'n_neighbors':range(1,40,2)}, df,['pc1','pc2'],'label','check')
# BEST PARAMS {'n_neighbors': 29} # Accuracy on training data: 0.93
# Accuracy on test data: 1.00
plt.figure(figsize=(20,15))
ax = plt.gca()
points_plot(ax, Xtrain, Xtest, ytrain, ytest, bestcv, alpha=0.5, psize=20);

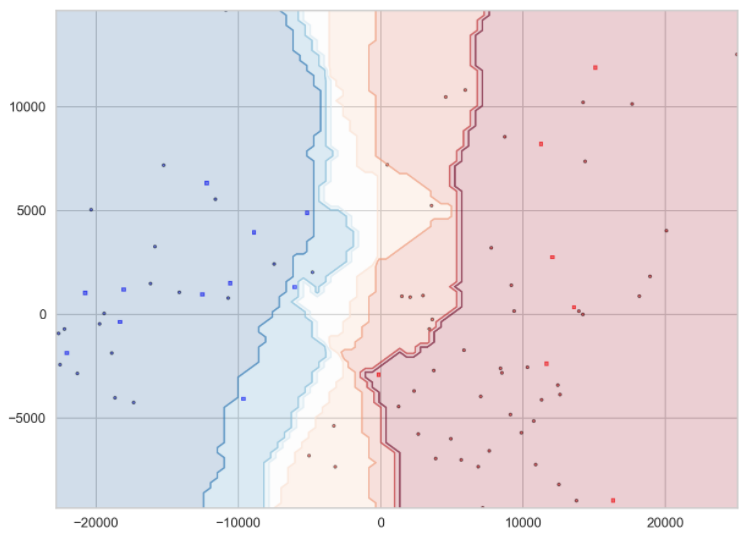
확률 등고선도 표시할 수 있다 : 빨간색이나 파란색의 이웃 비율을 세기만 하면 확률을 쉽게 얻을 수 있다.
plt.figure(figsize=(20,15))
ax = plt.gca()
points_plot_prob(ax, Xtrain, Xtest, ytrain, ytest, bestcv, alpha=0.5, psize=20)
Evaluation
from sklearn.metrics import confusion_matrix, classification_report
confusion_matrix(ytest, bestcv.predict(Xtest),)
#array([[ 6, 0],
[ 1, 11]], dtype=int64)