Machine Learning(Harvard)

Learning a Model

%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
pd.set_option('display.width',500)
pd.set_option('display.max_columns',100)
pd.set_option('display.notebook_repr_html',True)
import seaborn as sns
sns.set_style('whitegrid')
sns.set_context('poster')

def make_simple_plot():
    fig, axes=plt.subplots(figsize=(12,5), nrows=1, ncols=2);
    axes[0].set_ylabel("$y$")
    axes[0].set_xlabel("$x$")
    axes[1].set_xlabel("$x$")
    axes[1].set_yticklabels([])
    axes[0].set_ylim([-2,2])
    axes[1].set_ylim([-2,2])
    plt.tight_layout();
    return axes
def make_plot():
    fig, axes=plt.subplots(figsize=(20,8), nrows=1, ncols=2);
    axes[0].set_ylabel("$p_R$")
    axes[0].set_xlabel("$x$")
    axes[1].set_xlabel("$x$")
    axes[1].set_yticklabels([])
    axes[0].set_ylim([0,1])
    axes[1].set_ylim([0,1])
    axes[0].set_xlim([0,1])
    axes[1].set_xlim([0,1])
    plt.tight_layout();
    return axes

The process of learning

learning a model

우리가 선거와 같은 인간의 과정을 예측하려고 노력한다고 하자. 여기서 가난, 인종, 종교성과 같은 경제적, 사회학적 요인들이 중요하다. 그러한 요인과 선거 결과 사이에는 역사적 상관관계가 있으며, 이러한 상관관계를 모델에 통합하고자 할 수 있다. 이러한 모델의 예는 다음과 같다:

Romney가 승리할 확률은 인구의 종교성, 인종, 빈곤, 교육, 그리고 다른 사회적, 경제적 지표의 함수이다.

이 모델에 동기를 부여하는 우리의 인과적 주장은 아마도 종교인들이 사회적으로 더 보수적이고 따라서 공화당에 투표할 가능성이 더 높다는 것일 것이다. 이것은 정확한 인과관계는 아닐 수 있지만, 예측에 전적으로 중요한 것은 아니다. 상관관계가 존재하는 한, 우리의 모델은 무작위성 50-50보다 더 구조화되어 있고, 우리는 예측하고 시도할 수 있다.

예측되는 변수(예:Romny 후보의 투표확률)를 문자 $y$로 나타내며, 이 확률에서 입력으로 사용되는 특징이나 공변수를 문자 $x$로 나타낸다. 이 $x$는 다차원적일 수 있고, $x_1$은 가난, $x_2$는 인종 등이 될 수 있다.

$$ y = f(x) $$

A real simple model

Romney에게 투표할 확률은 카운티 내 인구가 얼마나 종교적인지에 대한 기능일 뿐인 매우 단순한 모델을 생각해 보자.

$x$를 카운티에서 종교인 비율, $y$를 $x$ 함수로 Romney에게 투표할 확률로 가정한다. 즉, $y_i$는 여론조사기관에서 가져간 데이터이며, 이는 Romney에게 투표한 사람들의 추정치를 말해주는 것이며, $x_i$는 카운티 $i$의 종교인 비율이다. 여론조사 샘플은 유한하기 때문에 각 데이터 포인트 또는 카운티 $i$에 대한 오차 한계가 있지만, 지금은 무시한다.

우리가 200개 카운티 x의 '인구'를 가지고 있다고 가정해보자.

df = pd.read_csv('religion.csv')
df.head()

plt.figure(figsize=(20,15))
x = df.rfrac.values
f = df.promney.values
plt.plot(x,f,'.')

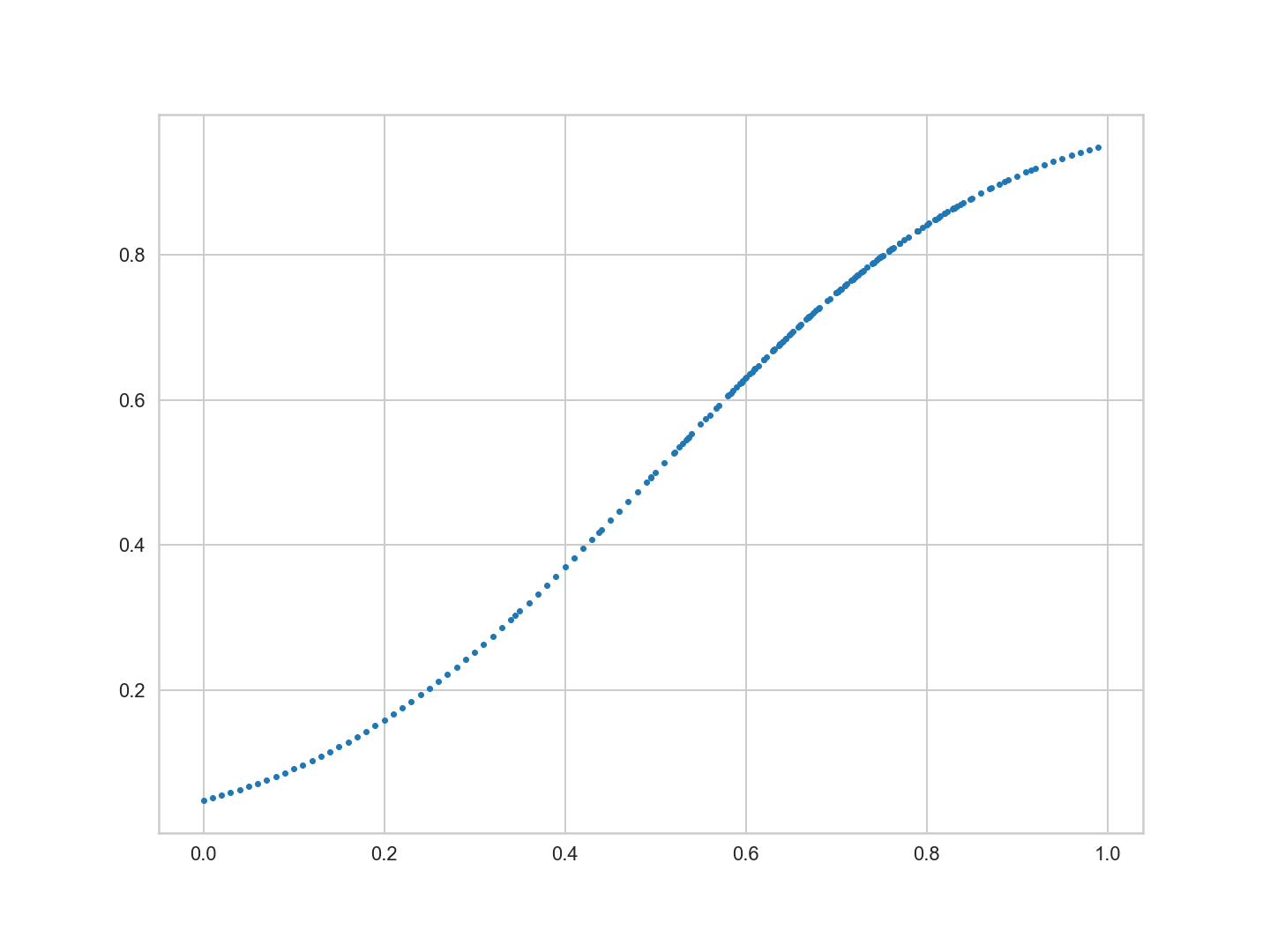
plot을 보면 x의 표본 추출이 균일하지 않다. 0.7 주위에 x의 점이 더 많다.

실생활에서 우리는 단지 점들의 샘플만을 받는다. 이 200개의 점 모집단 중에서 30개의 데이터 점 표본 $\cal{D}$가 주어졌다고 가정하자. 이러한 데이터를 표본 내 데이터라고 한다. 대조적으로 데이터 점의 전체 모집단을 표본 외 데이터라고 한다.

indexes = np.sort(np.random.choice(x.shape[0], size=30, replace=False))

samplex = x[indexes]
samplef = f[indexes]

plt.figure(figsize=(20,15))
axes = make_plot()
axes[0].plot(x, f, 'k-', alpha = 0.6, label = "f (from the Lord)");
axes[0].plot(x, f, 'r.', alpha = 0.2, label = 'population');
axes[1].plot(samplex, samplef, 's', alpha = 0.6, label = 'in-sample data $\cal{D}$');
axes[0].legend(loc=4);
axes[1].legend(loc=4);

오른쪽 패널 그림의 옅은 음영 사각형은 주어진 30개의 점의 표본 내 $\cal{D}$이다. 왼쪽 패널의 빨간 곡선은 잊어버린 척하자. 따라서, 우리가 아는 것은 오른쪽에 있는 곡선이고, 우리는 원래의 곡선이 무엇인지에 대한 단서도 없고, 원래의 '인구'도 기억하지 못한다.

즉, 우리가 목표 기능을 알지 못하고 오히려 약간의 데이터만 가지고 학습의 일반적인 경우라는 것을 기억하자. 따라서 우리가 할 일은 이러한 기능들 중 하나가 $f$에 근접할 수 있다는 희망으로 볼 수 있는 30개의 데이터 포인트를 생성할 수 있는 기능을 찾고 미래 데이터에 대한 예측 모델을 제공하는 것이다. 이를 데이터 적합이라고 한다.

The Hypothesis or Model Space

데이터를 적합시키는 데 사용하는 이러한 함수를 가설(hypothesis) 이라고 한다. 우리는 가설을 나타내기 위해 표기법 $h$를 사용할 수 있다. 위의 데이터에 대한 가설, 즉 다항식이라는 특정 함수 클래스를 가정해보자.

다항식은 x의 여러 거듭제곱을 선형으로 결합하는 함수이다.

\begin{align*} h(x) &=& 9x - 7 && ,(straight, line) \ h(x) &=& 4x^2 + 3x + 2 && ,(quadratic) \ h(x) &=& 5x^3 - 31x^2 + 3x && ,(cubic). \end{align*}

일반적으로 다항식은 다음과 같이 쓸 수 있다 :

\begin{eqnarray*} h(x) &=& a_0 + a_1 x^1 + a_2 x^2 + ... + a_n x^n \ &=& \sum_{i=0}^{n} a_i x^i \end{eqnarray*}

따라서 선형으로 계수 $a_i$ 곱하기 $x$의 거듭제곱, $x^i$의 합을 의미한다. 즉, 다항식은 계수에서 선형이다.

데이터를 적합시키는 데 사용한 함수, 즉 직선인 가설 $h$를 고려해보자. 우리는 데이터를 1차 다항식 또는 직선으로 적합시키고 있음을 나타내기 위해 첨자 $1$을 $h$에 넣었다. 이것은 다음과 같다 :

$$ h_1(x) = a_0 + a_1 x $$

최적 맞춤 직선을 함수 $g_1(x)$라고 한다. '최적합' 아이디어는 다음과 같다 :

모든 선 집합(즉, $h_1(x)$의 가능한 모든 선택) 중에서 샘플 내 데이터를 나타내는 가장 적합한 라인 $g_1(x)$은 무엇인가? ($g$의 첨자 $1$은 데이터에 가장 적합한 라인 중 가장 적합한 다항식을 나타내기 위해 선택된다.)

최적 접합 $g_1(x)$는 아래 그림과 같다.

plt.figure(figsize=(20,15))
g1 = np.poly1d(np.polyfit(x[indexes],f[indexes],1))
plt.plot(x[indexes],f[indexes], 's', alpha=0.6, label='in-sample');
plt.plot(x, g1(x), 'b--', alpha=0.6, label="$g_1$");
plt.legend(loc=4)

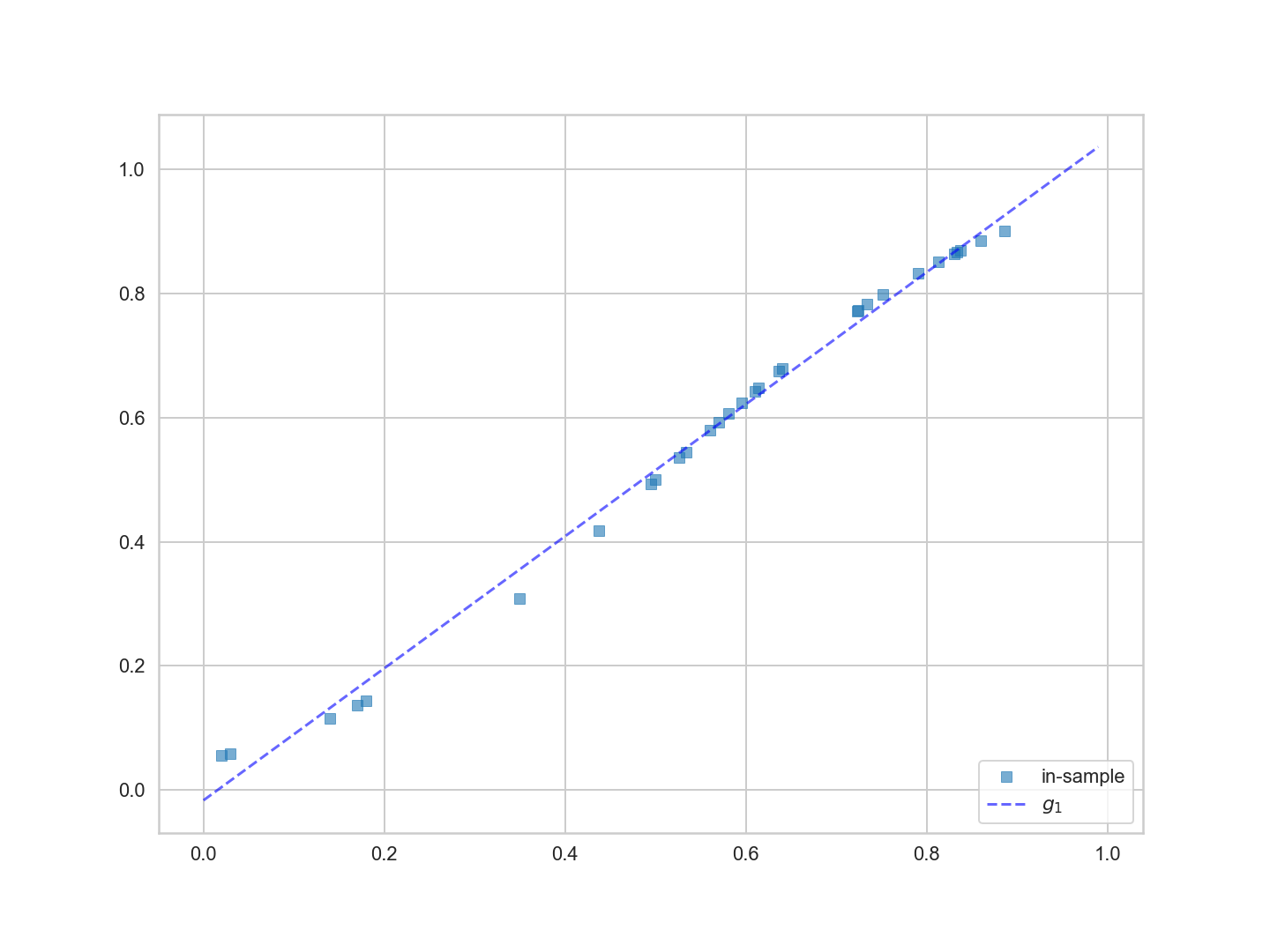
우리가 어떻게 가장 적합한지 계산했을까? '선들 사이에 가장 적합한 선'이라는 개념을 조금 공식화하고 일반화해 보자.

데이터를 적합시키는 데 사용할 수 있는 특정 종류의 모든 함수의 집합을 **가설 공간($\cal{H}$)**이라고 한다.

모든 직선 $h_1(x)$의 가설 공간을 고려하자. 다항식의 순서를 표시하기 위해 첨자를 사용하여 $\cal{H}_1$로 표시한다. 이러한 또 다른 공간은 모든 2차 함수의 가설 공간인 $\cal{H}_2$일 수 있다. 3번째는 이 두가지를 결합할 수 있다. 따라서 우리는 우리의 가설 공간에 넣고 싶은 것을 선택할 수 있다.

우리는 가설 공간 $\cal{H}_1$ 함수에서 데이터 $\cal{D}$에 대한 최상의 $g_1$를 발견했다. 이것은 가능한 모든 기능에서 가장 잘 맞는 것이 아니라 모든 직선 집합에서 가장 잘 맞는 것이다.

가설 공간은 데이터를 적합시키는 데 사용하는 모형의 복잡도를 캡처하는 데 사용하는 개념이다. 예를 들어, 2차식은 직선보다 복잡하므로(곡선이 더 많음), $\cal{H}_2$는 $\cal{H}_1$보다 더 복잡한 개념이다.

이 경우, 실제 모델을 생각하지 않고, 우리는 데이터의 추세를 나타내는 가장 단순한 가설 공간인 직선의 집합을 사용하기로 결정한다.

Deterministic Error or Bias

위의 그림에서 볼 때 $\cal{H}_1$의 모델, 즉 직선 및 특히 최적 직선 $g_1$은 데이터의 곡선(우리가 근사하려고 하는 기본 함수 $f$)를 캡처하는 데 그다지 도움이 되지 않는다.

아래 그림에서 보다 일반적인 경우를 생각해보자. 곡선 $f$는 $f$가 가지는 꿈틀거림이 없는 함수 $g$로 근사치이다.

그러면 근사치에는 항상 오류가 있을 것이다. 이 근사 오차는 파란색 음영 영역과 그 bias 또는 deterministic error로 그림에 표시된다.

이전 이름은 $g$가 $f$ 하는 방식으로 움직이지 않는 사실에서 비롯되었다. 후자의 이름은 대부분의 학습 상황에서와 같은 목표 함수 $f$를 모를 경우 이 오류를 측정 및 노이즈와 같은 다른 오류와 구별하는 데 어려움을 겪을 수 있다는 개념에서 비롯되었다.

현재 모델로 돌아가 보면, 직선 $\cal{H}1$ 공간이 데이터 곡선을 캡처하지 못한다는 것이 분명하다. 따라서 20차 다항식 $h{20}(x)$의 집합인 좀 더 복잡한 가설 공간 $\cal{H}_{20}$을 생각해 보자 :

$$h_{20}(x) = \sum_{i=0}^{20} a_i x^i,.$$

보다 복잡한 가설 공간이 어떻게 작용하는지 보기 위해, 가장 적합한 20차 다항식 $g_{20}(x)$를 찾아보자.

g20 = np.poly1d(np.polyfit(x[indexes],f[indexes],20))

plt.figure(figsize=(20,15))
plt.plot(x[indexes], f[indexes], 's', alpha=0.6, label='in-sample');
plt.plot(x, g20(x), 'b--', alpha=0.6, label='$g_{20}$');
plt.legend(loc=4)

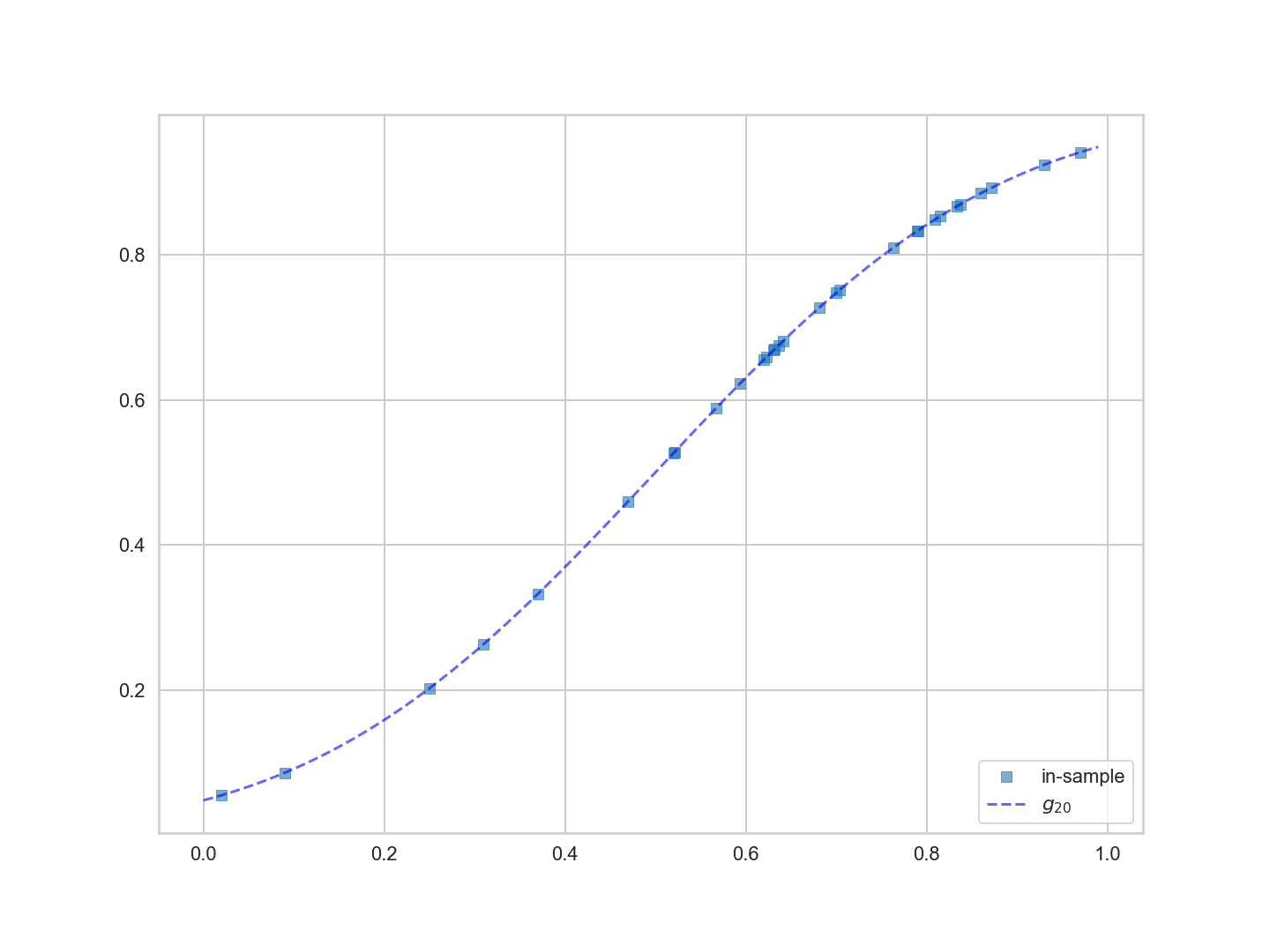
20차 다항식이 점들을 더 잘 추적하는 것을 볼 수 있다. 왜냐하면 직선이 아닌 모든 점들을 '가까이 가거나 통과' 할 수 있는 공간을 가지고 있기 때문이다. 따라서 $\cal{H}_{20}$가 최적 적합 모형을 선택하는 데 더 적합한 후보 가설 집합일 수 있다.

$g_1$과 $g_{20}$ 모두에 대한 편향의 개념을 계산하여 이를 계량화할 수 있다. 이를 위해 200점 모집단에서 f와 g의 차이의 제곱을 계산한다.

$$B_1(x) = (g_1(x) - f(x))^2 ,;,, B_{20}(x) = (g_{20}(x) - f(x))^2,.$$

제곱은 우리가 양의 양을 계산하고 있다는 것을 확실히 한다.

plt.figure(figsize=(20,15))
plt.plot(x, (g1(x)-f)**2, lw=3, label='$B_1(x)$')
plt.plot(x, (g20(x)-f)**2, lw=3, label='$B_{20}(x)$');
plt.xlabel('$x$')
plt.ylabel('population error')
plt.yscale('log')
plt.legend(loc=4)
plt.title('Bias')

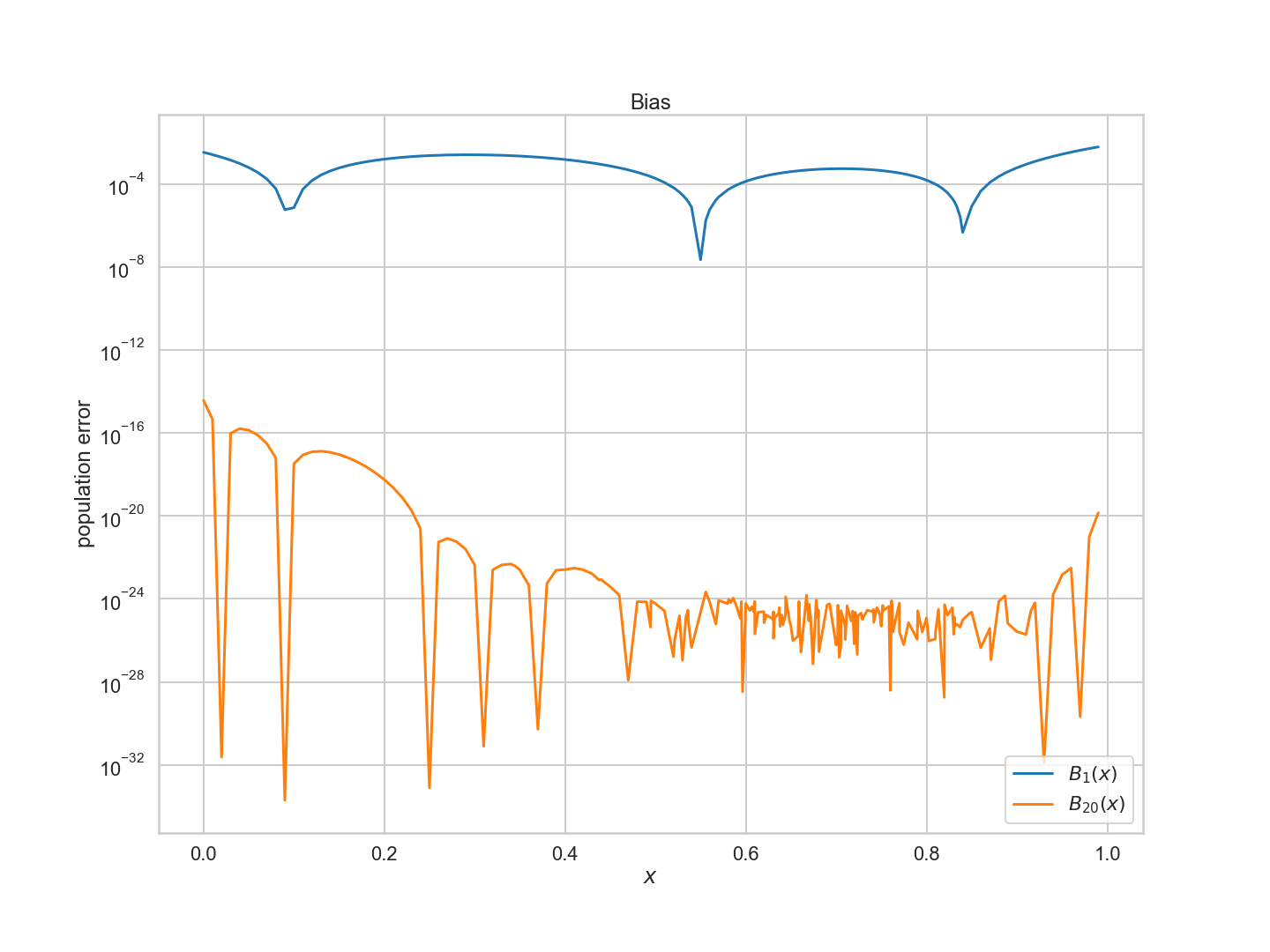
보시다시피 $g_{20}$에 대한 편향 또는 근사 오차가 훨씬 작다.

$g_{20}$이 가능한 모든 모델의 이 데이터에 가장 적합한 모델인가? 실제로, 우리는 어떻게 가장 좋은 가설 공간에서 가장 적합한 모델을 찾을 수 있을까? 이것이 학습의 핵심이다.

우리는 파이썬 함수 'np.polyfit'을 사용하여 $g_{1}$은 $\cal{H}{1}$에서, $g{20}$은 $\cal{H}_{20}$에서 가장 적합한 모델을 찾았지만, 어떻게 그러한 결론에 도달했을까? 이것이 다음 장의 주제이다.

How to learn the best fit model in a hypothesis space

함수가 데이터에 적합하다는 것이 무엇을 의미하는지 직관적으로 이해해보자. 지금은 모든 직선의 집합인 $\cal{H}_{1}$ 가설 공간만 고려하자. 아래 그림에서 우리는 데이터 포인트(빨간색)에 대해 이러한 선 $h_1(x)$(빨간색)를 그린다.

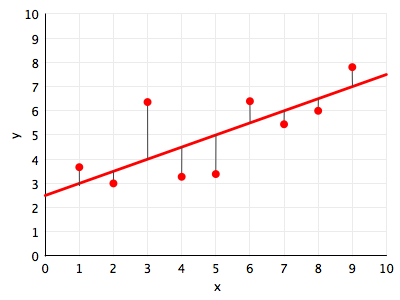
'최적합'에 대해 생각하는 자연스러운 방법은 거리 개념의 경우 선에서 점까지의 거리를 최소화하는 것이다. 도표에서 우리는 거리에 대한 한 가지 개념을 묘사한다 : 점에서 선까지의 수직거리. 이러한 거리는 얇은 검은색 선으로 표시된다.

그 다음에 제기되는 질문은 이것이다. 이 수직 거리의 측정치를 정확히 어떻게 정의할 수 있을까? 우리는 거리에 대한 양의 추정치를 측정치로 사용해야 한다. 거리의 절대값인 $\vert y_i - h_1(x_i) \vert$ 또는 거리 제곱 $(y_i - h_1(x_i))^2$을 측정치로 사용할 수 있다. 둘 다 합리적인 선택이지만 거리 제곱을 사용하고자 한다.

$y_i$ in $\cal{D}$에 맞추기 위해 선 $h_1(x)$을 사용하는 오류 함수 또는 위험 함수(오류, 비용 또는 위험이라고도 함)로 알려진 것을 생성하기 위해 모든 데이터 지점에 걸쳐 이 측정값을 요약한다 :

$$ R_{\cal{D}}(h_i(x)) = \frac{1}{N} \sum_{y_i \in \cal{D}} (y_i - h_1(x_i))^2 $$

여기서 $N$은 $\cal{D}$의 점 수다.

이 공식에 따르면 비용 또는 위험은 관측 지점으로부터 직선까지의 거리를 제곱한 것이다. 여기서 함수라는 단어는 함수 프로그래밍에서와 마찬가지로 위험이 함수 $h_1(x)$의 함수 임을 나타낸다.

위험의 값은 관찰한 지점에 따라 달라지기 때문에 샘플 내 데이터 $\cal{D}$도 명시한다. 이러한 관찰을 $x_i$의 다른 집합에서 $y_i$로 했다면 위험의 가치는 다소 다를 것이다.

이제, 이러한 관측치와 가설 공간 $\cal{H}_1$을 고려할 때, 우리는 최적의 적합 함수 $g_1(x)$를 찾기 위해 가설 공간의 가능한 모든 함수에 대한 위험을 최소화한다 :

$$ g_1(x) = \arg\min_{h_1(x) \in \cal{H}} R_{\cal{D}}(h_1(x)).$$

여기서 $\cal{H}$는 함수의 일반적인 가설 공간이다.

The role of sampling

우리의 샘플이 대표적이어야 한다. 보다 정확하게는 모집단의 훈련점 표본(또는 우리가 예측하고자 하는 새로운 x)이 대표적이어야 한다.

200개의 데이터 포인트 모집단과 30개의 데이터 포인트 표본(초록색)에 대해 아래 설명을 참조하라.

plt.figure(figsize=(20,15))
plt.hist(x, bins=30, alpha=0.7)
sns.kdeplot(x)
plt.plot(x[indexes], [1.0]*len(indexes),'o', alpha=0.8)
plt.xlim([0,1])
plt.ylim([0,20])

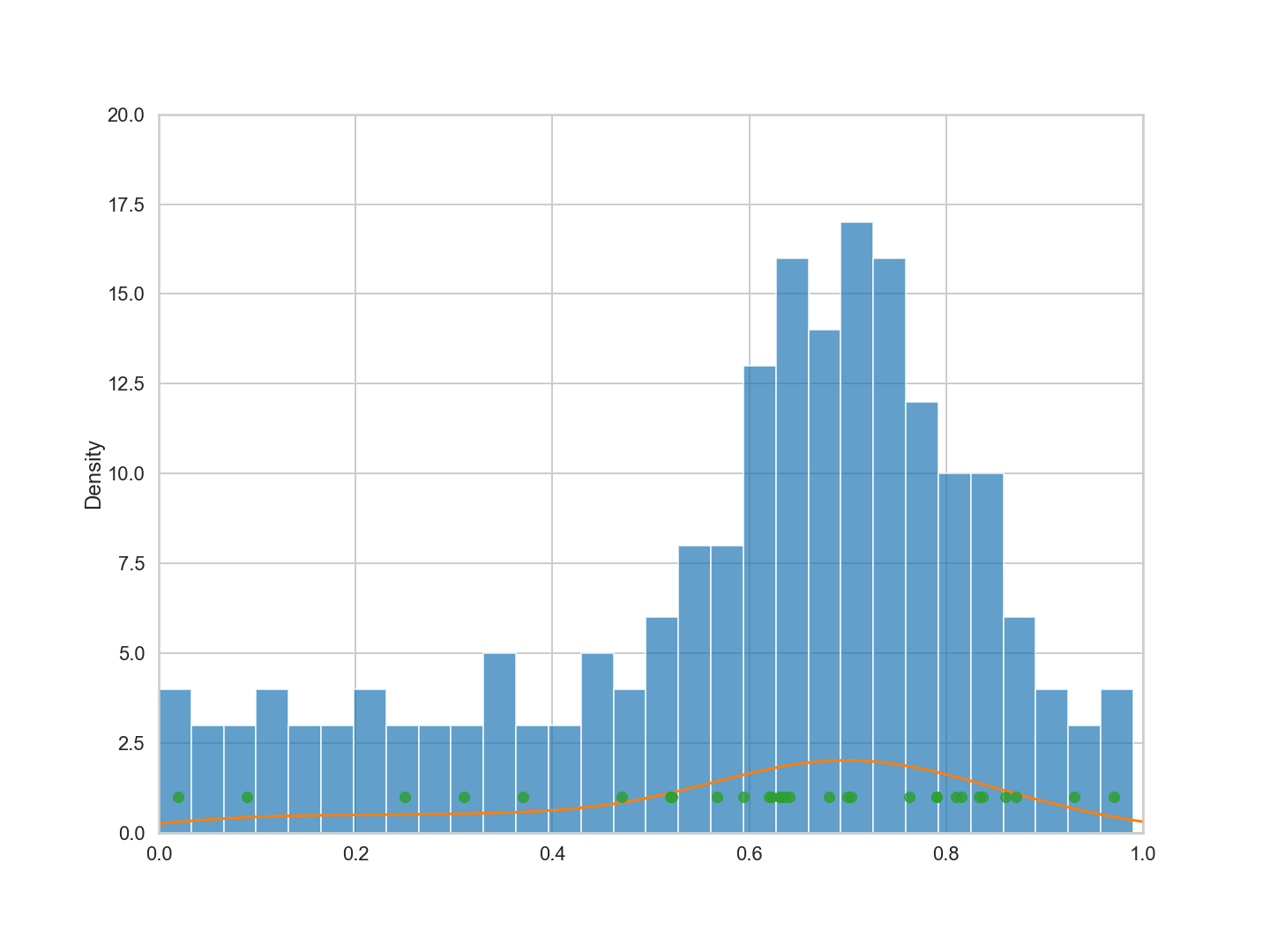
이 예제에서 큰 $x$ 또는 더 종교적인 카운티에 대해 예측하기 위해 $f$의 추정치인 $g$만 사용하려면 점 $x$에 1에 가까운 표본 추출이 필요하다. 마찬가지로 예측을 위해 사용하는 새로운 $x$도 해당 카운티를 대표해야 한다. 만약 우리가 저종교 국가를 고종교 국가들의 표본으로부터 예측하려고 노력한다면, 우리는 잘하지 못할 것이다. 또는 전체 종교성 범위를 예측하려면 교육 샘플이 $x$ 모두를 더 잘 커버할 수 있다.

초록색 점은 히스토그램을 잘 따르는 것 같다.

Statement of the learning problem

우리가 직관적으로 훈련 세트에 대한 비용이나 위험을 최소화하는 가설 $g$를 발견한다면, 이 가설은 훈련 세트가 대표하는 모집단에 대해 잘 작동할 수 있을 것이다. 왜냐하면 모집단에 대한 위험은 훈련 세트에 대한 위험과 비슷해야 하고 따라서 작아야 하기 때문이다.

수학적으로 우리는 다음과 같이 말하고 있다 :

\begin{eqnarray*} A &:& R_{\cal{D}}(g) ,,smallest,on,\cal{H}\ B &:& R_{out ,of ,sample} (g) \approx R_{\cal{D}}(g) \end{eqnarray*}

즉, 경험적 위험이 표본 위험의 범위를 잘 추정하여 표본 위험의 범위도 작아야 한다.

실제로, 우리가 아래에서 볼 수 있듯이, $g_{20}$는 표본뿐만 아니라 모집단에서도 탁월한 효과를 발휘한다.

plt.figure(figsize=(20,15))
plt.plot(x, g20(x), 'b--', alpha=0.9, lw=2, label='$g_{20}$')
plt.plot(x, f, 'o', alpha=0.2, label='population')
plt.legend(loc=4)

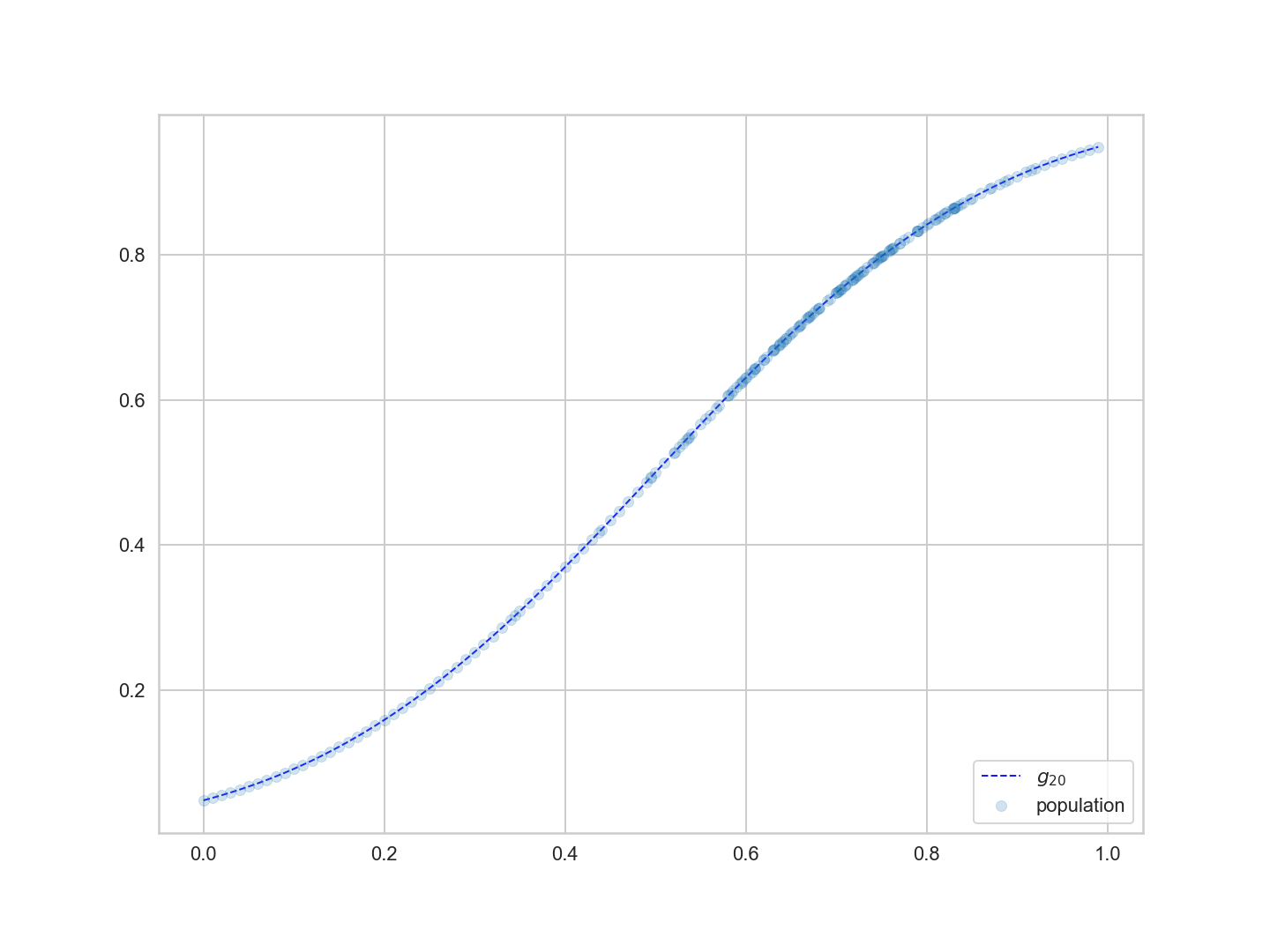
Noise

1.2.11 정확도(Accuracy) 측정하기우리는 위의 다이어그램에서 $g_{20}$가 모집단의 곡선을 잘 포착했다는 것을 보았다. 그러나 목표인 $f$에서 얻은 데이터는 여전히 매우 매끄러웠다. 대부분의 실제 데이터 세트는 측정 오류, 기타 공변량 등과 같은 다양한 효과 때문에 전혀 매끄럽지 않다. 이러한 탄성 소음은 곧 알게 되지만 우리의 발작에 지장을 준다.

Stochastic Noise, or the problem with randomness

확률적 소음은 인간에게 알려진 거의 모든 데이터 세트를 악화시키며, 여러 가지 다른 이유로 발생한다.

예를 들어 신용 이력과 급여가 동일한 은행의 두 고객을 생각해보자. 한 사람은 담보대출을 연체하고 다른 사람은 연체하지 않는다. 이 경우 이 두 고객에 대한 동일한 $x = (신용, 급여)$가 있지만,$y$가 다르다. $y$는 고객이 채무 불이행한 경우 1이고 그렇지 않은 경우 0이다. 여기서 진정한 $y$는 부부 싸움, 부모의 질병 등과 같은 다른 공변인의 함수일 수 있다. 하지만, 은행으로서, 우리는 이 정보를 가지고 있지 않을 수도 있다. 따라서 우리가 가지고 있는 정보 x에서 고객마다 다른 $y$를 받는다.

비슷한 일이 선거 사례에서도 일어날 수 있는데, 우리는 Romney에게 투표할 확률을 카운티의 종교성의 함수로 모델링했다. 하지만 우리가 측정하지 않았을지도 모르는 다른 변수들이 많이 있다. 예를 들어, 해당 카운티의 다수당 경선이다. 그러나 우리는 이 정보를 측정하지 않았다. 따라서 종교성 비율이 $x$인 카운티에서는 다른 카운티보다 noise가 더 많을 수 있다. 예를 들어, 두 개의 카운티를 생각해보자. 하나는 카운티에서 스스로 식별된 종교인의 $x=0.8$ 퍼센트를 가진 카운티이고 다른 하나는 $x=0.82$를 가진 카운티이다. 역사적인 추세에 따르면, 만약 첫 번째 카운티가 대부분 백인이었다면, 그들이 Romney에게 투표할 것이라고 주장하는 사람들의 비율은 두 번째, 대부분 흑인 카운티의 비율보다 더 클지도 모른다. 따라서 그래프에서 두 개의 $y$가 서로 옆에 있을 수 있다.

그것은 악화된다. 여론조사기관들이 특정 후보에게 투표하는 사람들의 수를 추정할 때, 그들은 유권자들의 한정된 표본만을 사용한다. 따라서 이 추정치들 중 어느 것에도 4~6%의 여론조사 오류가 있다. 이 'sampling noise'는 $y$의 noise를 더한다.

실제로 $y_i$ 값이 함수 $f$에서 나오도록 함수 $f(x)$를 추정하고자 한다. 일부 카운티의 데이터만으로 f를 추정하려고 하고 있으며, 게다가 이러한 카운티의 인구 행동에 대한 추정치는 noisy함으로, 우리의 추정시는 noisy 추정치가 될 것이다.

이러한 오류가 학습 과정에 어떤 영향을 미치는지 시뮬레이션해 보겠다.

sigma = 0.06
mask = (x > 0.65) & (x < 0.8)
sigmalist = sigma + mask*0.03

y = f + sp.stats.norm.rvs(scale=sigmalist, size=200)
yadd = (y < 0.0) * (0.01 - y)
ysub = (y > 1.0) * (y - 1.0)
y = y + yadd - ysub

plt.figure(figsize=(20,15))
plt.plot(x, f, 'r-', alpha=0.6, label='f');
plt.plot(x[indexes], y[indexes], 's', alpha=0.6, label='in-sample y (observed)');
plt.plot(x, y, '.', alpha=0.6, label='population y');
plt.xlabel('$x$');
plt.ylabel('$p_R$')
plt.legend(loc=4);

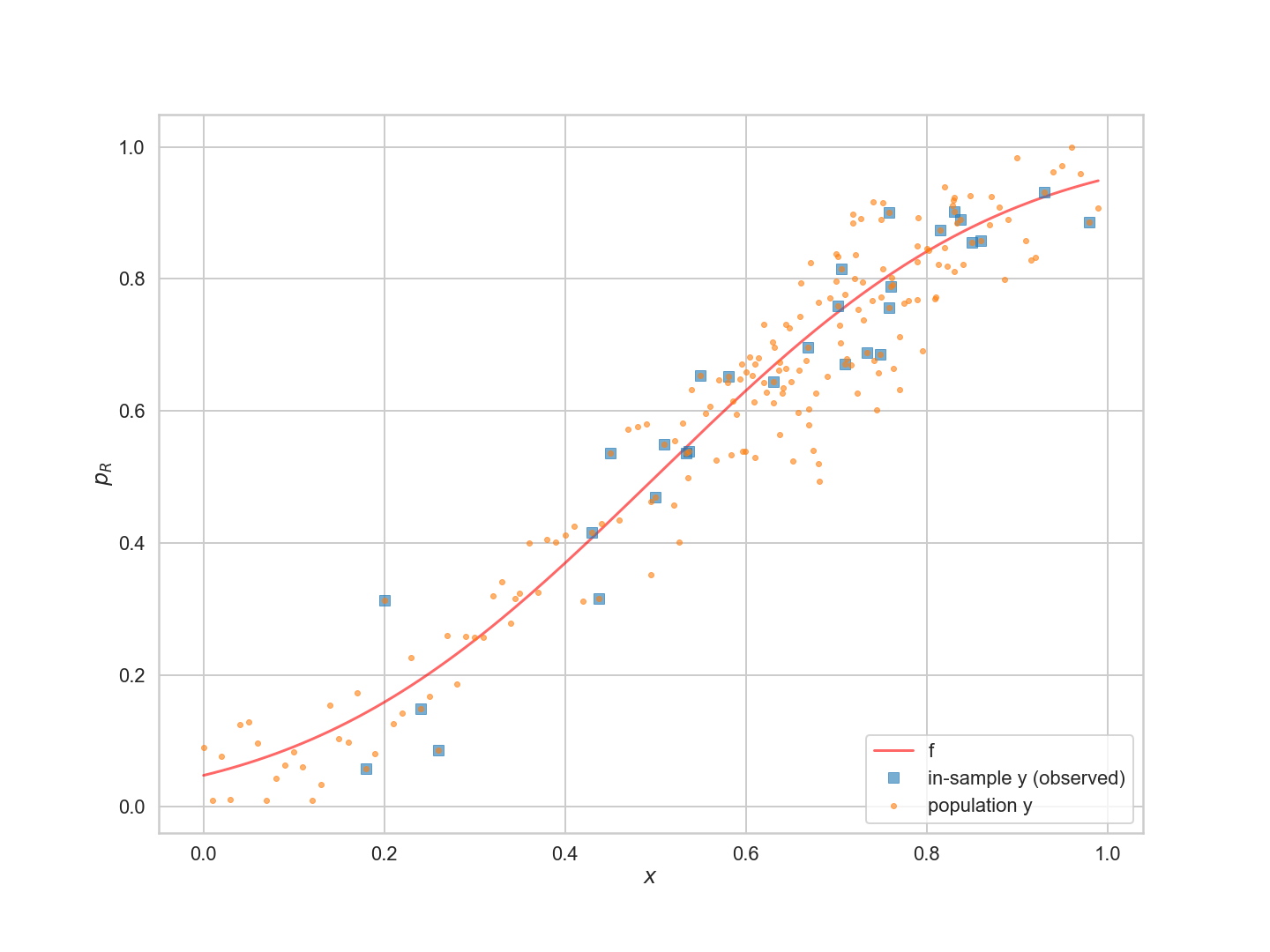
위의 그림에서 $f$ 곡선에 대한 $y$ 모집단의 산포를 볼 수 있다. 30개의 관측점('표본 내')의 오차는 제곱으로 표시된다. 위에서 설명한 것처럼 서로 옆에 있는 관측치가 상당히 다를 수 있음을 알 수 있다.

Fitting a noisy model : the complexity of your hypothesis

이제 직선($\cal{H}1$) 및 20차 다항식($\cal{H}{20}$)을 사용하여 위에서 시뮬레이션한 노이즈 데이터를 적합해 보자.

우리가 한 것은 잡음이 많은 목표 $y$를 도입하여,

$$y = f(x) + \epsilon,,$$

여기서 $\epsilon$는 확률적 노이즈를 나타내는 랜덤 노이즈 용어이다. 위의 오류 시뮬레이션에서 우리는 $\epsilon$이 종 곡선에서 도출되었다고 가정했다. 이는 $\epsilon$이 종 곡선에서 선택한 값과 함께 다른 $x$에서 다르다는 것을 의미한다.

노이즈가 많은 $y$에 대해 생각하는 또 다른 방법은 데이터가 공동 확률 분포 $P(x,y)$에서 생성된다고 가정하는 것이다. 확률적 노이즈가 없는 이전의 경우, 일단 $x$를 알고 나면, 만약 $f(x)$를 준다면, 정확히 $y$를 줄 수 있다. 이것은 이제 노이즈 $\epsilon$ 때문에 가능하지 않다 : 우리는 주어진 $x$에서 얼마나 많은 노이즈가 있는지 정확히 모른다. 따라서 확률 분포(이 예에서는 벨 곡선)를 사용하여 $P(y|x)$로 작성된 지정된 $x$에서 $y$를 모델링해야 한다. $P(x)$도 확률 분포이므로 다음과 같이 할 수 있다 :

$$P(x,y) = P(y | x) P(x) .$$

이제 전체 학습 문제가 확률 밀도 추정의 문제로 제시될 수 있다. 위험 또는 오류 기능 덕분에 $P(x,y)$를 추정하고 해당 추정치를 기반으로 조치를 취하면 된다.

이제 각각 가장 적합한 직선과 가장 적합한 20차 다항식을 찾기 위해 $\cal{H}1$ 및 $\cal{H}{20}$에 모두 적합한다.

g1noisy = np.poly1d(np.polyfit(x[indexes], y[indexes],1))
g20noisy = np.poly1d(np.polyfit(x[indexes], y[indexes],20))

plt.figure(figsize=(20,15))
axes = make_plot()
axes[0].plot(x, f, 'r-', alpha=0.6, label='f');
axes[1].plot(x, f, 'r-', alpha=0.6, label='f');
axes[0].plot(x[indexes], y[indexes], 's', alpha=0.6, label='y in-sample');
axes[1].plot(x[indexes], y[indexes], 's', alpha=0.6, label='y in-sample');
axes[0].plot(x,g1(x), 'b--', alpha=0.6, label='$g_1 (no noise)$');
axes[0].plot(x, g1noisy(x), 'b:', lw=4, alpha=0.8, label='$g_1 (noisy)$');
axes[1].plot(x,g20(x), 'b--', alpha=0.6, label='$g_10 (no noise)$');
axes[1].plot(x,g20noisy(x), 'b:', lw=4, alpha=0.8, label='$g_{10}$ (noisy)');
axes[0].legend(loc=4);
axes[1].legend(loc=4);

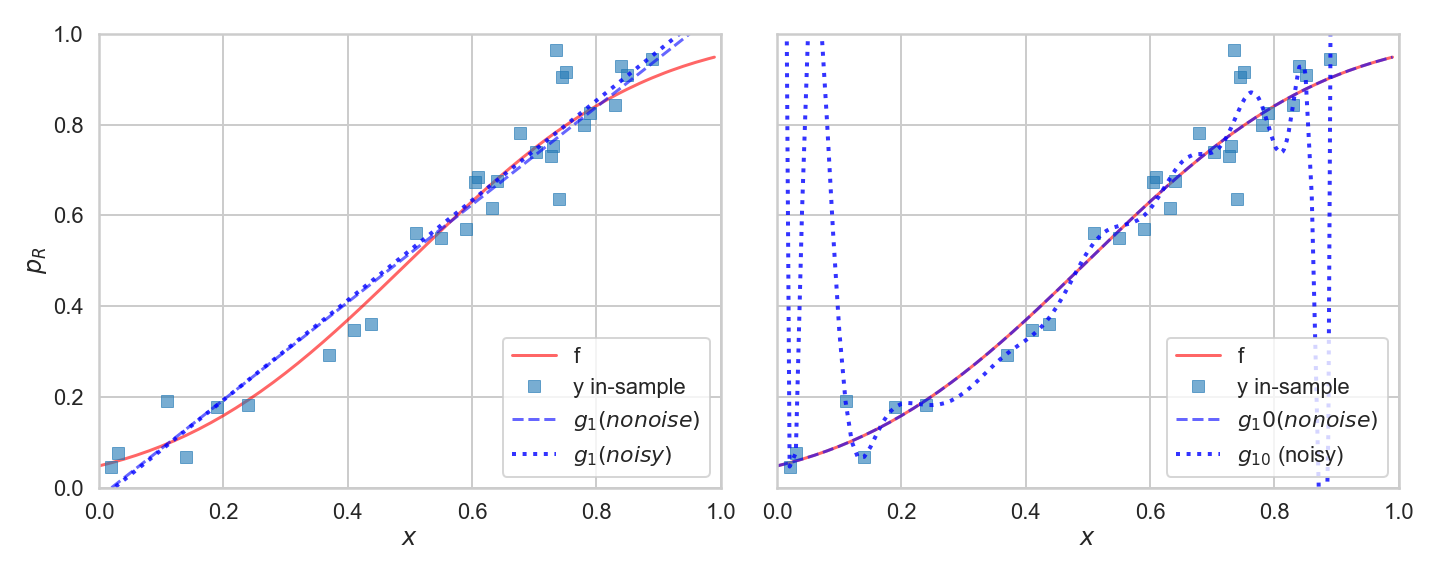
왼쪽의 그림을 보게 되면, 노이즈는 최적 적합선을 조금씩 변경하지만 크게 변경하지는 않는다. 최적 적합선은 여전히 데이터의 변동을 포착하는 데 매우 약하다.

잡음이 있을 때 가장 적합한 20차 다항식은 관측치의 모든 곡선을 따르려고 한다. 다시 말해서, 그것은 노이즈에 맞추려고 노력한다.

plt.figure(figsize=(20,15))
plt.plot(x, f, 'r-', alpha=0.6, label='f');
plt.plot(x[indexes], y[indexes], 's', alpha=0.6, label='y in-sample');
plt.plot(x, y, '.', alpha=0.6, label='population y');
plt.plot(x, g20noisy(x), 'b:', alpha=0.6, label='$g_{10}$ (noisy)');
plt.ylim([0,1])
plt.legend(loc=4);

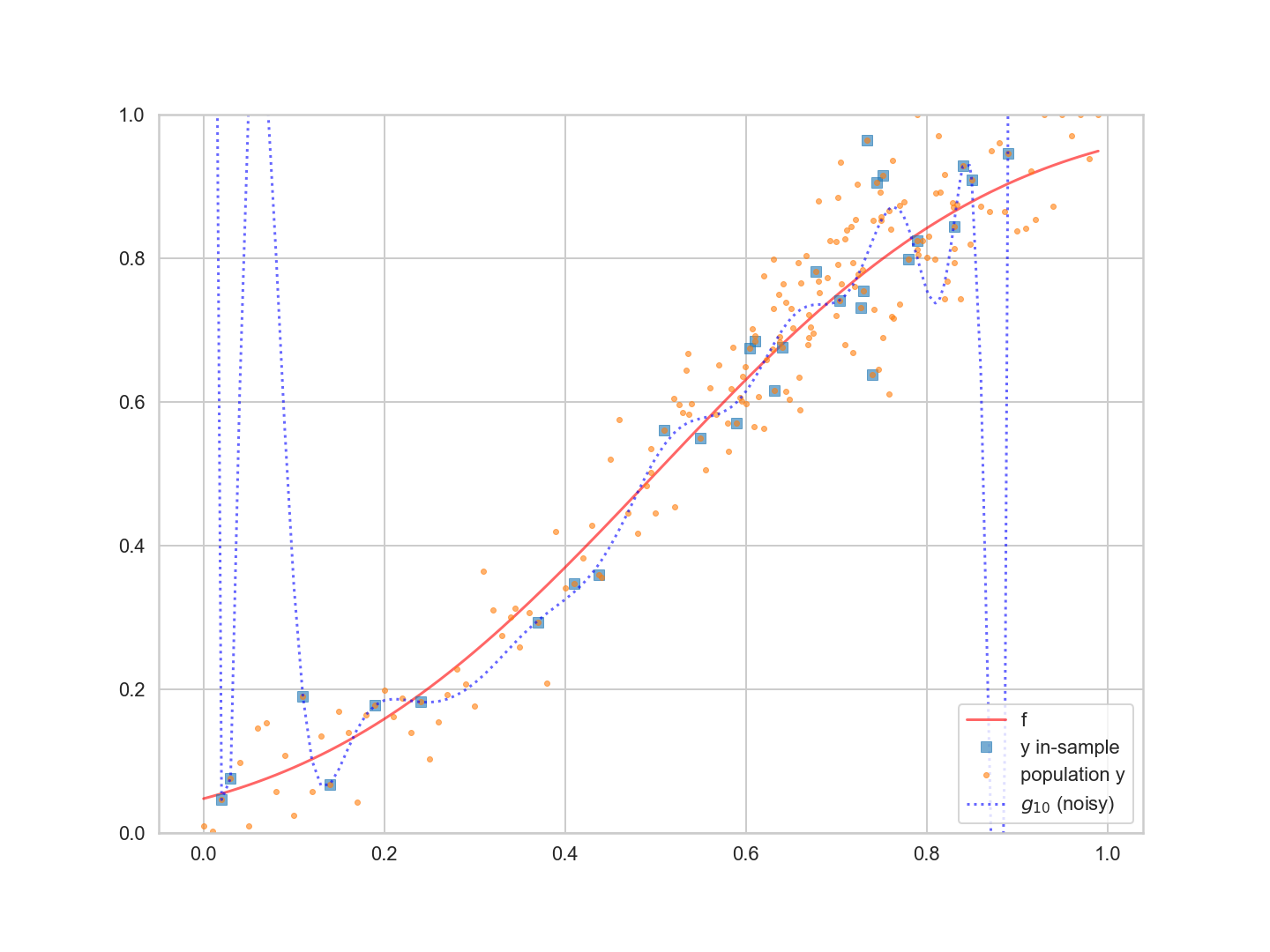
최적 적합 20차 다항식은 표본 내 데이터를 적합시키는 데 합리적인 역할을 하며 표본 내 데이터 점이 많은 중간 지점에서도 잘 작동한다.그러나 표본 내 데이터 포인트가 적은 곳에서는 다항식이 미친 듯이 꿈틀거린다.

이러한 노이즈에 적합한 것은 학습 중에 반복적으로 직면하게 될 위험이다. 이것을 과적합이라고 한다. 따라서 잡음이 없을 때 매우 좋은 후보 가설 공간인 것처럼 보였던 $\cal{H}_{20}$은 1이 되는 것을 멈춘다. 여기서 얻을 수 있는 교훈은 우리 모델이 노이즈에 맞지 않도록 더욱 확실히 해야 한다는 것이다.

앞서 결정론적 노이즈에 대해 작성한 것과 유사한 그래프를 작성하고 노이즈가 많은 데이터에 대한 새로운 $g1$ 및 $g20$ 적합치의 오류를 비교해보자.

plt.figure(figsize=(20,15))
plt.plot(x, ((g1noisy(x) - f) ** 2), lw=3, label='$g_1$')
plt.plot(x, ((g20noisy(x) - f) ** 2), lw=3, label='$g_{20}$');
plt.plot(x, [1]*x.shape[0], 'k:', label='noise', alpha=0.2);
for i in indexes[:-1]:
    plt.axvline(x[i], 0, 1, color='r', alpha=0.1)
plt.axvline(x[indexes[-1]], 0, 1, color='r', alpha=0.1, label='samples')
plt.xlabel('$x$')
plt.ylabel('population error')
plt.yscale('log')
plt.legend(loc=4);
plt.title('Noisy Data');


대부분의 경우 $g_1$에서 오류가 더 낮다. 따라서 노이즈가 많은 데이터, 복잡한 모델($\cal{H}_{20}$)보다 훨씬 더 많은 편향(직선, $\cal{H}_1$)을 가진 모델 세트를 선택하는 것이 더 나을 것이다.

The Variance of your model

노이즈를 적합시킬 수 있는 충분한 자유도를 가지면서 보다 복잡한 모형이 과대 적합되는 경향을 고분산이라고 한다. 분산이란 무엇인가?

간단히 말해서 분산은 모집단에서 추출한 다른 데이터 집합 $\cal{D}_1, \cal{D}_2,...$에 대한 훈련을 통해 학습되는 모델의 '오류 막대' 또는 확산이다.

그러나 어쨌든 여기서 데이터를 시뮬레이션했으므로, 200개의 모집단에서 무작위로 30개의 다른 점을 선택하고 $\cal{H}1$ 및 $\cal{H}{20}$의 모델을 둘 다 맞추면 어떻게 되는지 보자. 우리는 각각 30개의 점으로 이루어진 랜덤하게 선택된 200개의 데이터 세트에 대해 이 작업을 수행하고 200개 집합에 대해 가설 공간에 가장 적합한 모형을 표시한다.

def gen(degree, nsims, size, x, out):
    outpoly=[]
    for i in range(nsims):
        indexes = np.sort(np.random.choice(x.shape[0], size=size, replace=False))
        pc = np.polyfit(x[indexes], out[indexes], degree)
        p = np.poly1d(pc)
        outpoly.append(p)
    return outpoly

polys1 = gen(1,200,30,x,y);
polys20 = gen(20,200,30,x,y)

axes = make_plot()
axes[0].plot(x, f, 'r-', lw=3, alpha=0.6, label='f');
axes[1].plot(x, f, 'r-', lw=3, alpha=0.6, label='f');
axes[0].plot(x[indexes], y[indexes], 's', alpha=0.6, label='data y');
axes[1].plot(x[indexes], y[indexes], 's', alpha=0.6, label='data y');
axes[0].plot(x,y,'.',alpha=0.6, label='population y');
axes[1].plot(x,y,'.',alpha=0.6, label='population y');
c = sns.color_palette()[2]
for i,p in enumerate(polys1[:-1]):
    axes[0].plot(x,p(x),alpha=0.05,c=c)
axes[0].plot(x,polys1[-1](x), alpha=0.05, c=c, label='$g_1$ from different samples')
for i,p in enumerate(polys20[:-1]):
    axes[1].plot(x,p(x),alpha=0.05,c=c)
axes[1].plot(x,polys20[-1](x), alpha=0.05, c=c, label='$g_{10}$ from different samples')
axes[0].legend(loc=4);
axes[1].legend(loc=4);

왼쪽 패널에 200개의 최적 맞춤 직선이 있고 각 직선은 200개의 점 모집단과 다른 30개의 점 훈련 세트에 적합한다. 최적 적합선은 $f$(두꺼운 빨간색 선) 또는 데이터(제곱)를 잘 캡처하지 못하더라도 함께 모인다.

오른쪽 패널에서, 우리는 $\cal{H}_{20}$에서 선택한 최적의 모델에서 동일한 것을 볼 수 있다. 대부분의 모델은 여전히 실제 곡선 $f$와 데이터 $y$의 중심 추세를 따라 이동하지만, 상당한 양의 모델은 모든 종류의 잡음이 많은 머리카락으로 이동한다. 이는 분산이다 : 주어진 $x$의 예측 값은 어디에나 있다.

분산은 다항식 적합 계수를 표시하여 다른 방법으로 확인할 수 있다. 아래에는 $\cal{H}_1$의 적합 계수가 표시된다. 두 co-efficients에 대한 평균에 대한 분산은 거의 0.2이다.

#pdict1={}
#pdict20={}
#for i in reversed(range(2)):
    #pdict1[i]=[]
    #for j, p in enumerate(polys1):
        #pdict1[i].append(p.c[i])
#for i in reversed(range(21)):
    #pdict20[i]=[]
    #for j, p in enumerate(polys20):
        #pdict20[i].append(p.c[i]) 
#df1=pd.DataFrame(pdict1)
#df20=pd.DataFrame(pdict20)
#fig = plt.figure(figsize=(14, 5)) 
#from matplotlib import gridspec
#gs = gridspec.GridSpec(1, 2, width_ratios=[1, 10]) 
#axes = [plt.subplot(gs[0]), plt.subplot(gs[1])]
#axes[0].set_ylabel("value")
#axes[0].set_xlabel("coeffs")
#axes[1].set_xlabel("coeffs")
#plt.tight_layout();
#sns.violinplot(df1, ax=axes[0]);
#sns.violinplot(df20, ax=axes[1]);
#axes[0].set_yscale("symlog");
#axes[1].set_yscale("symlog");
#axes[0].set_ylim([-1e12, 1e12]);
#axes[1].set_ylim([-1e12, 1e12]);
# 코드 실행이 안됨

오른쪽 패널에 $\cal{H}_{20}$의 적합 계수를 표시한다. 이것이 우리가 '분산'이라는 단어를 사용하는 이유이다. 즉, 평균에 대한 중간 계수 값(dashed lines)의 산포는 큰 특이치가 있는 $10^{10}$(팽창의 수직 높이)이다.

지금까지

• 학습 문제의 기본 공식화, 가설 공간의 개념, 그리고 이 가설 공간에서 목표 함수에 가장 적합한 모델을 찾기 위해 거리의 최소화(비용 또는 위험이라고 함)를 사용하는 전략을 배움
• 노이즈가 이러한 적합성에 미치는 영햑과 학습 대상 기능에 발생하는 문제들은 데이터로부터 배움. 주로 이 노이즈에 지나치게 적합한 문제들임.

학습 과정에는 두 가지 부분이 있다 :

1. 표본 내 위험을 최소화하여 모형에 적합
2. 표본 내 위험이 표본 외 위험과 잘 유사하기를 바라는 것

우리가 샘플의 일부를 보류하고 이 보류된 부분에 시험해봄으로써 학습자의 성과를 테스트할 수 있다. 따라서 보류된 부분 또는 표본의 '검정' 부분에 대한 오류나 위험을 계산하여 표본 외 오차에 대해 설명할 수 있다.

Testing and Training Sets

우리는 주어진 데이터 $\cal{D}$의 샘플을 채취하여 두 부분으로 나눈다 :

1. 모델을 적합시키는 데 사용하는 데이터의 일부인 교육세트
2. 데이터 세트의 작은 부분인 테스트 세트는 적합도가 얼마나 좋은지 확인하는 데 사용된다.

이 분할은 이 두 집합에서 무작위로 점을 선택하여 수행된다. 일반적으로 데이터의 80%를 교육 세트에 넣고, 나머지 양은 테스트 세트에 넣을 수 있다. 이 작업은 sklearn.cross_validation의 train_test_split 함수를 사용하여 파이썬에서 수행할 수 있다.

분할은 아래 다이어그램에 나와 있다.

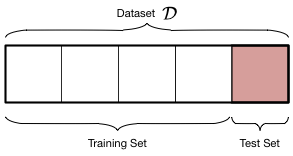
모델을 교육하기 위해 필요한 데이터의 양에 타격을 받고 있다. 데이터가 많을수록 적합성에 더 도움이 된다. 그러나 학습자가 학습한 것과 동일한 데이터를 보고 학습자의 일반화 능력을 파악할 수는 없다. 일반화할 것이 없고, 보간기와 같이 일반화할 희망이 없는 매우 복잡한 모델을 훈련 데이터에 맞출 수 있다. 따라서 표본 외 오차 또는 위험을 추정하려면 이 추정치를 만들기 위해 데이터를 남겨야 한다.

우리는 교육 세트를 샘플 내 세트로 사용하고 테스트 세트를 샘플 외에 대한 proxy로 사용하고 있다.

df = pd.DataFrame(dict(x=x[indexes],f=f[indexes],y=y[indexes]))

from sklearn.model_selection import train_test_split
datasize=df.shape[0]
# split dataset using the index, as we have x,f, and y that we want to split.
itrain, itest = train_test_split(range(30), train_size=24, test_size=6)
xtrain = df.x[itrain].values
ftrain = df.f[itrain].values
ytrain = df.y[itrain].values
xtest = df.x[itest].values
ftest = df.f[itest].values
ytest = df.y[itest].values

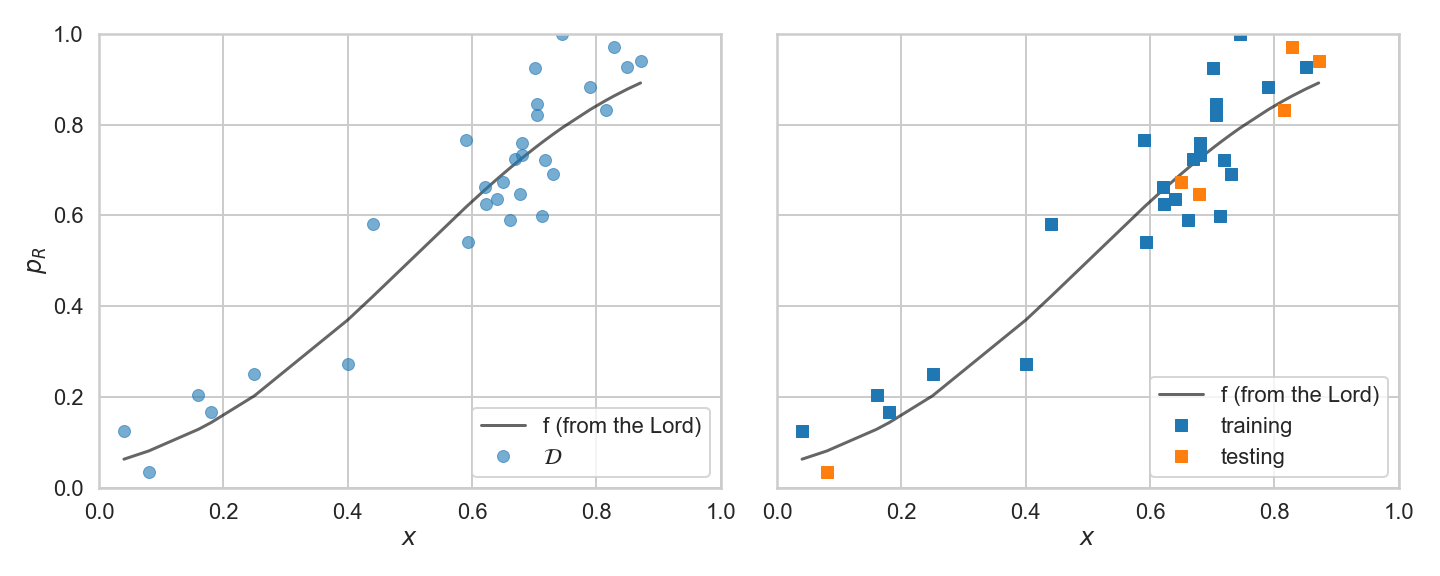
axes = make_plot()
axes[0].plot(df.x, df.f, 'k-', alpha=0.6, label='f (from the Lord)');
axes[0].plot(df.x, df.y, 'o', alpha=0.6, label='$\cal{D}$');
axes[1].plot(df.x, df.f, 'k-', alpha=0.6, label='f (from the Lord)');
axes[1].plot(xtrain, ytrain, 's', label='training')
axes[1].plot(xtest, ytest, 's', label='testing')
axes[0].legend(loc='lower right')
axes[1].legend(loc='lower right')

A short digression about scikit-learn

Scikit-learn은 주요 파이썬 머신러닝 라이브러리이다. 그것은 train_test_split과 같은 많은 유틸리티 기능뿐만 아니라 데이터로부터 모델을 배울 수 있는 많은 학습자로 구성되어 있다.

라이브러리에는 인터페이스가 매우 잘 정의되어 있다 : scikit-learn 내의 모든 객체는 모델 구축 분석을 위한 추정기 인터페이스, 예측을 하기 위한 예측기 인터페이스 및 데이터 변환을 위한 변압기 인터페이스의 세 가지 보완적 인터페이스로 구성된 균인한 공통 기본 API를 공유한다.

이전에 파이썬 함수 polyfit을 사용하여 y에 맞췄다. Scikit-learn에 익숙해지도록 하기 위해 여기서는 '추정기' 인터페이스, 특히 추정기 다항식 특징을 사용할 것이다.

우선, 한 카운티의 종교인 비율 x를 예로 들자면, 그 카운티의 Romney에게 투표하는 비율 y를 예측하기 위해 사용하고자 한다. 우리가 할 일은 변화이다 :

$$ x \rightarrow 1, x, x^2, x^3, ..., x^d $$

어떤 파워 $d$에 대하여 우리의 일은 다항식의 이러한 특징의 계수에 적합하는 것이다.

$$ a_0 + a_1 x + a_2 x^2 + ... + a_d x^d. $$

다시 말해서, 우리는 한 형상의 함수를 많은 형상의 (다소 단순한) 선형 함수로 변환했다. 이를 위해 먼저 추정기를 다항식 형상(d)으로 구성한 다음 fit_transtrom 방법을 사용하여 이러한 형상을 d차원 공간으로 변환한다.

따라서 항상 samples는 행, 열은 features를 의미한다.

[1,2,3]이 아닌 [1], [2], [3]을 사용하는 이유는 scikit-learn이 데이터가 크기 [n_샘플, n_특징]의 2차원 배열이나 행렬에 저장될 것으로 예상하기 때문이다.

from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures(3).fit_transform([[1],[2],[3]])

[1,2,3]을 [[1],[2],[3]]으로 바꾸려면 모양을 바꿔야 한다.

np.array([1,2,3]).reshape(-1,1)

그래서 이제 우리는 scikit-learn이 기대하는 사각형, rows=samples, columns=features 형태에 있다. 그러면 1-D 데이터 세트 x를 d차원 데이터 세트로 변환하는 과정을 살펴보자.

xtrain

xtrain.reshape(-1,1)

PolynomialFeatures(2).fit_transform(xtrain.reshape(-1,1))

이 모은 것을 종합해 보자. 아래에서는 각 다항식 차수에 하나씩 여러 데이터 세트를 생성한다.

def make_features(train_set, test_set, degrees):
    traintestlist = []
    for d in degrees:
        traintestdict = {}
        traintestdict['train'] = PolynomialFeatures(d).fit_transform(train_set.reshape(-1,1))
        traintestdict['test'] = PolynomialFeatures(d).fit_transform(test_set.reshape(-1,1))
        traintestlist.append(traintestdict)
    return traintestlist

How do training and testing error change with complexity?

다항식 차수를 증가시키고 차원 d를 증가시키기 위해 training 세트에 선형 회귀 모델을 적합시킨다. 그런 다음 scikit-learn을 사용하여 오류나 위험을 계산한다. 우리는 훈련 집합과 검정 집합 모두에서 모델의 예측과 데이터 사이의 평균 제곱 오차를 계산한다. 우리는 이 오류를 다항식 d의 정의 함수로 표시한다.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

degrees = range(21)
error_train = np.empty(len(degrees))
error_test = np.empty(len(degrees))

traintestlists = make_features(xtrain, xtest, degrees)

The structure of scikit-learn

fit은 항상 두 개의 인수를 사용한다 :

estimator.fit(Xtrain, ytrain)

여기서 Xtrain은 배열 배열의 형태여야 하며, 내부 배열은 각각 하나의 샘플에 해당하고, 그 요소의 요소는 해당 샘플의 형상 값에 해당한다. (이것은 다항식 예제에서 각 배열의 네 번째 요소는 각 'sample' $x$의 $x^3$ 값에 해당한다는 것을 의미한다.) ytrain은 응답의 단순한 배열이다. 회귀 문제의 경우 연속형, 분류 문제의 경우 범주형 값의 경우 1-0이다.

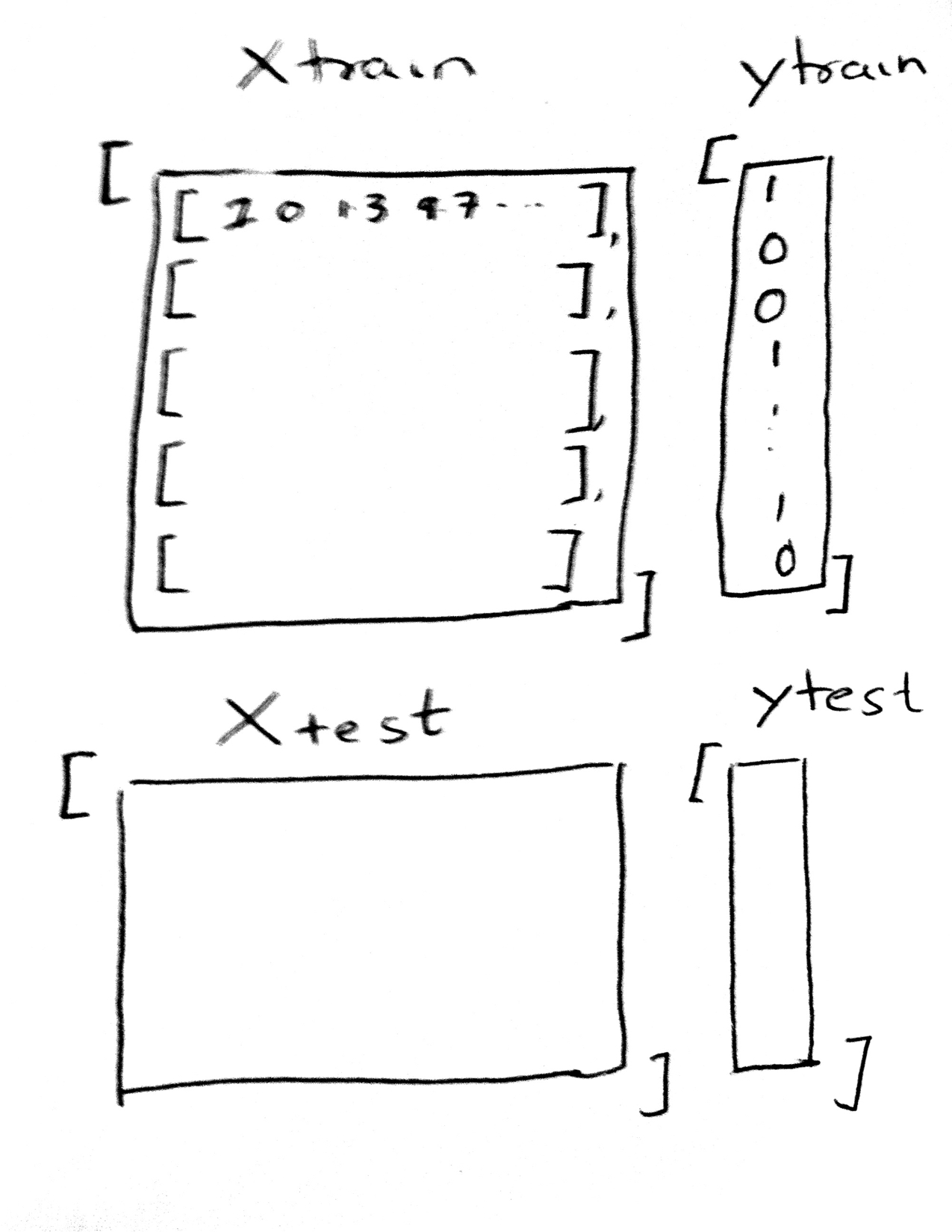
traintestlists[3]['train'], ytrain

테스트 세트 Xtest는 구조가 동일하며 예측 인터페이스에 사용된다. 추정기를 적합시키면 다음 방법으로 테스트 결과를 예측할 수 있다.

estimator.predict(Xtest)

결과는 ytest와 형태 및 형태가 동일한 단순한 예측 배열이다.

traintestlists[3]['test'], ytest

그런 다음 sklearn의 평균 제곱 오차를 사용하여 예측과 실제 ytest 값 사이의 오차를 계산할 수 있다. 아래에서는 훈련 세트(이미 적합)와 테스트 세트(이전에는 보지 못했던) 모두에서 이 오류를 계산하고 이러한 오류가 다항식의 정도에 따라 어떻게 변하는지 그림으로 표시한다.

# for increasing polynomial degrees 0,1,2 ...
plt.figure(figsize=(20,15))
for d in degrees:
    Xtrain = traintestlists[d]['train']
    Xtest = traintestlists[d]['test']
    # set up model
    est = LinearRegression()
    # fit
    est.fit(Xtrain, ytrain)
    # predict
    prediction_on_training = est.predict(Xtrain)
    prediction_on_test = est.predict(Xtest)
    # calculate mean squared error
    error_train[d] = mean_squared_error(ytrain, prediction_on_training)
    error_test[d] = mean_squared_error(ytest, prediction_on_test)
    
plt.plot(degrees, error_train, marker='o', label='train (in-sample)')
plt.plot(degrees, error_test, marker='o', label='test')
plt.axvline(np.argmin(error_test), 0, 0.5, color='r', 
            label='min test error at d=%d'%np.argmin(error_test),
           alpha=0.3)
plt.ylabel('mean squared error')
plt.xlabel('degree')
plt.legend(loc='upper left')
plt.yscale('log')

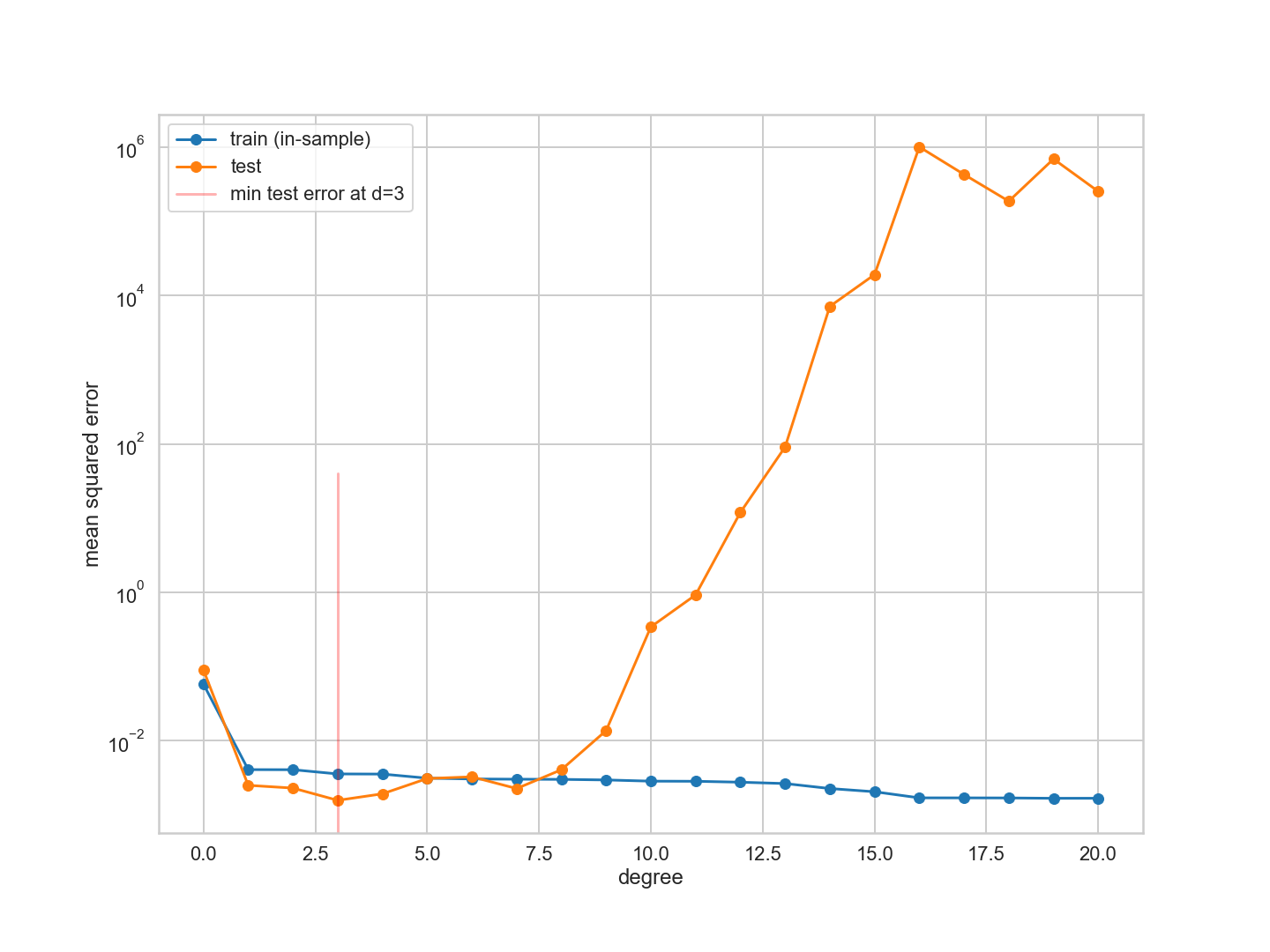
훈련 오류는 다항식의 차수가 증가함에 따라 감소한다. 우리는 모든 훈련 데이터에 맞게 임의로 복잡한 다항식을 구성할 수 있고, 실제로 훈련 세트에 있는 24개의 데이터 포인트를 완벽하게 보간하는 24차 다항식을 구성할 수 있다. 또한 모든 데이터 포인트를 캡처하는 것이 미친 듯이 흔들리기 때문에 테스트 세트에서는 매우 좋지 않다는 것을 알고 있다. 그리고 이것이 우리가 테스트 세트 오류에서 볼 수 있는 것이다.

$d=0$ 데이터의 평균값을 포착하는 평면선 또는 $d=1$과 같은 극히 낮은 차수의 다항식의 경우, 다항식은 데이터의 함축성을 포착할 만큼 곡선이 있지 않다. (underfitting) 우리는 치우침/ 결정론적 오류 체계에 있으며, 여기서 우리는 가설이 너무 단순하기 때문에 항상 데이터와 적합치 사이에 약간의 차이를 가진다.

그러나 4보다 높은 차수의 경우 다항식이 너무 많이 흔들리기 시작하여 훈련 데이터를 캡처할 수 없다. 다항식의 예측 검정력이 훈련 데이터를 적합시키기 위해 견뎌야 하는 기울기 때문에 떨어지면 검정 집합 오차가 증가한다. (overfitting)

따라서 시험 집합 오류는 모델이 더 표현력을 갖추게 될수록 먼저 감소하며, 그 다음 복잡성의 특정 수준(여기서 $d$로 색인화)을 초과하면 증가한다. 이 아이디어는 테스트 세트 오류 또는 위험을 최소화하는 가설로 최상의 가설을 선택하여 모델에서 적절한 양의 복잡성만 식별하는 데 사용될 수 있다. 우리의 경우, 이러한 현상은 $d=4$에서 발생한다. (이 정확한 숫자는 훈련 및 시험 집합에서 선택된 무작위 점에 따라 달라진다.) 도표의 빨간색 수직선으로 식별되는 이 임계치보다 낮은 복잡도의 경우 가설은 적합하지 않고 복잡도가 높을 경우 적합성이 초과된다.

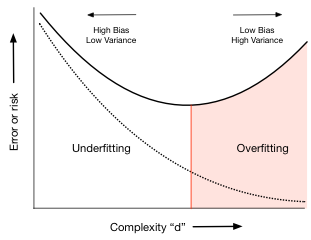
Validation

위의 프로세스에는 문제가 있다. $d=4$를 가장 좋은 가설로 꼽은 것은 테스트 세트를 교육 세트로 사용했기 때문이다.

우리의 프로세스는 훈련 세트 오류 최소화(경험적 위험 최소화)에 기초하여 주어진 $d$차수 다항식의 매개변수(계수 값)에 적합하도록 훈련 세트를 사용했다. 그런 다음 우리는 그 $d$에서 시험 세트의 오류를 계산했다. 더 나아가서 검정 집합 오차의 최소화에 기초하여 최적의 $d$를 선택하면, 검정 집합에서 $d$에 대해 '적합'이 된다. 따라서 우리는 $d$를 모델의 초 매개 변수라고 부를 것이다.

이 경우 검정 집합 오차는 실제 표본 외 오차를 과소평가한다. 또한 시험세트를 오염시켰다. 더 이상 실제 시험 세트가 아니다.

따라서 복잡성 매개 변수 $d$가 적합한 새로운 **검증 세트(Validation set)**를 도입해야 하며, 학습자의 실제 표본 외 성능을 추정하는 데 사용할 수 있는 테스트 세트를 제외해야 한다. 사물 체계에서 이 세트의 위치는 다음과 같다 :

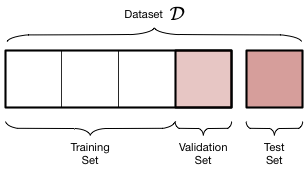
우리는 이전 훈련을 훈련 세트와 검증 세트로 나누었고, 복잡성 $d$에 대한 '적합'을 얻은 후 최종 테스트를 위해 이전 테스트를 제쳐놓았다. 분명 우리는 훈련에 사용할 수 있는 데이터의 크기를 더 줄였지만, 이는 테스트 위험 $\cal{E}{test}$ ($R{test}$)을 통해 표본 외 위험 $\cal{E}{out}$ ($R{out}$ 위험)의 좋은 추정치를 얻기 위해 지불해야 하는 댓가이다.

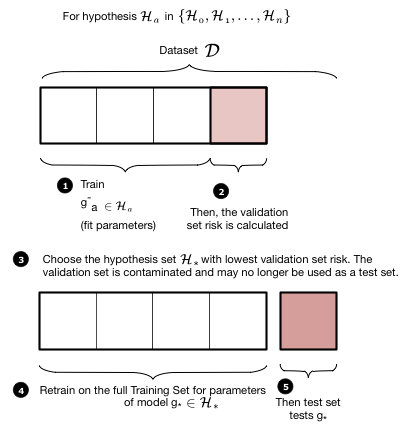
검증 프로세스는 이 두 그림에 설명되어 있다. 먼저 우리가 고려하고자 하는 모든 가설 집합을 반복한다 : 우리의 경우 이것은 복잡도 매개변수 $d$, 우리가 시도하고 맞출 다항식의 차수에 대한 반복이다. 그런 다음 $d$에 대해 '마이너스' 위첨자가 기존 훈련 세트에서 유효성 검사 청크(종종 테스트 청크와 같은 크기)를 제거하여 얻은 새 훈련 세트에 모델을 적합함을 나타내는 최적의 모델 $g^-d$을 얻는다. 그런 다음 이 모델을 검증 청크에서 '테스트'하여 최적 다항식 계수와 $d$에 대한 유효성 검사 오류를 얻는다. 다음 단계인 $d$로 넘어기 전과 같이 이 과정을 반복한다. 앞의 테스트 오류와 마찬가지로 모든 유효성 검사 세트 오류를 비교하고 이 유효성 검사 세트 오류를 최소화하는 $d*$ 등급을 선택한다.

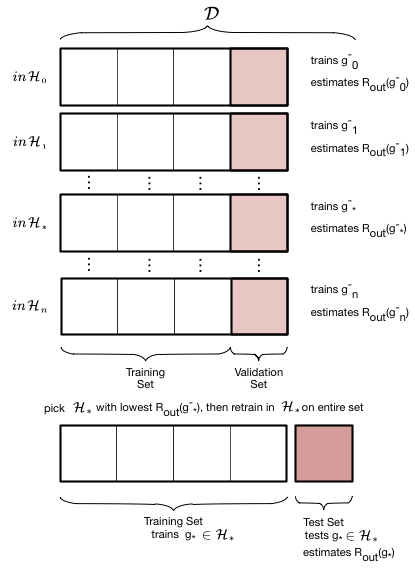
초 매개 변수 $d_$를 선택한 후, 우리는 전체 이전 훈련 집합에 대한 가설 집합 $\cal{H}_{}$를 사용하여 순서 $d_$의 다항식과 그에 상응하는 최적 접합 가설 $g_$의 매개 변수를 찾기 위해 재교육한다. $g$를 빼면 전체 이전 훈련 세트에 대해 훈련되었음을 알 수 있다. 이제 테스트 세트의 테스트 오류를 테스트 위험 $\cal{E}_{test}$의 추정치로 계산한다.

따라서 초 매개 변수가 적합할 경우 유효성 검사가 설정된다. 데이터 $\cal{D}$를 분할하는 방법을 train-validate-test split이라고 한다.

아래 교육/검증 분할에 대해 이 프로세스를 수행한다. 새 교육 세트의 작은 크기에 주목해보자. 테스트 세트도 같은 사이즈다.

# we split the training set down further
plt.figure(figsize=(20,15))
intrain, invalid = train_test_split(itrain, train_size=18, test_size=6)
xntrain = df.x[intrain].values
fntrain = df.f[intrain].values
yntrain = df.y[intrain].values
xnvalid = df.x[invalid].values
fnvalid = df.f[invalid].values
ynvalid = df.y[invalid].values

degrees = range(21)
error_train = np.empty(len(degrees))
error_valid = np.empty(len(degrees))
trainvalidlists = make_features(xntrain, xnvalid, degrees)

# for increasing polynomial degrees 0,1,2 ...
for d in degrees:
    # Create polynomials from x
    Xntrain = trainvalidlists[d]['train']
    Xnvalid = trainvalidlists[d]['test']
    # fit a model linear in polynomial coefficients on the new smaller training set
    est = LinearRegression()
    est.fit(Xntrain, yntrain)
    # predict on new training and validation sets and calculate mean squared error
    error_train[d] = mean_squared_error(yntrain, est.predict(Xntrain))
    error_valid[d] = mean_squared_error(ynvalid, est.predict(Xnvalid))

# Calculate the degree at which validation error is minimized
mindeg = np.argmin(error_valid)
ttlist = make_features(xtrain, xtest, degrees)

#fit on whole training set now
clf = LinearRegression()
clf.fit(ttlist[mindeg]['train'], ytrain) 

# predict on the test set now and calculate error
pred = clf.predict(ttlist[mindeg]['test'])
err = mean_squared_error(ytest, pred)
plt.plot(degrees, error_train, marker='o', label='train (in-sampel)')
plt.plot(degrees, error_valid, marker='o', label='validation')
plt.plot([mindeg], [err], marker='s', markersize=10, label='test', alpha=0.5, color='r')
plt.ylabel('mean squared error')
plt.xlabel('degree')
plt.legend(loc='upper left')
plt.yscale('log')
print(mindeg)

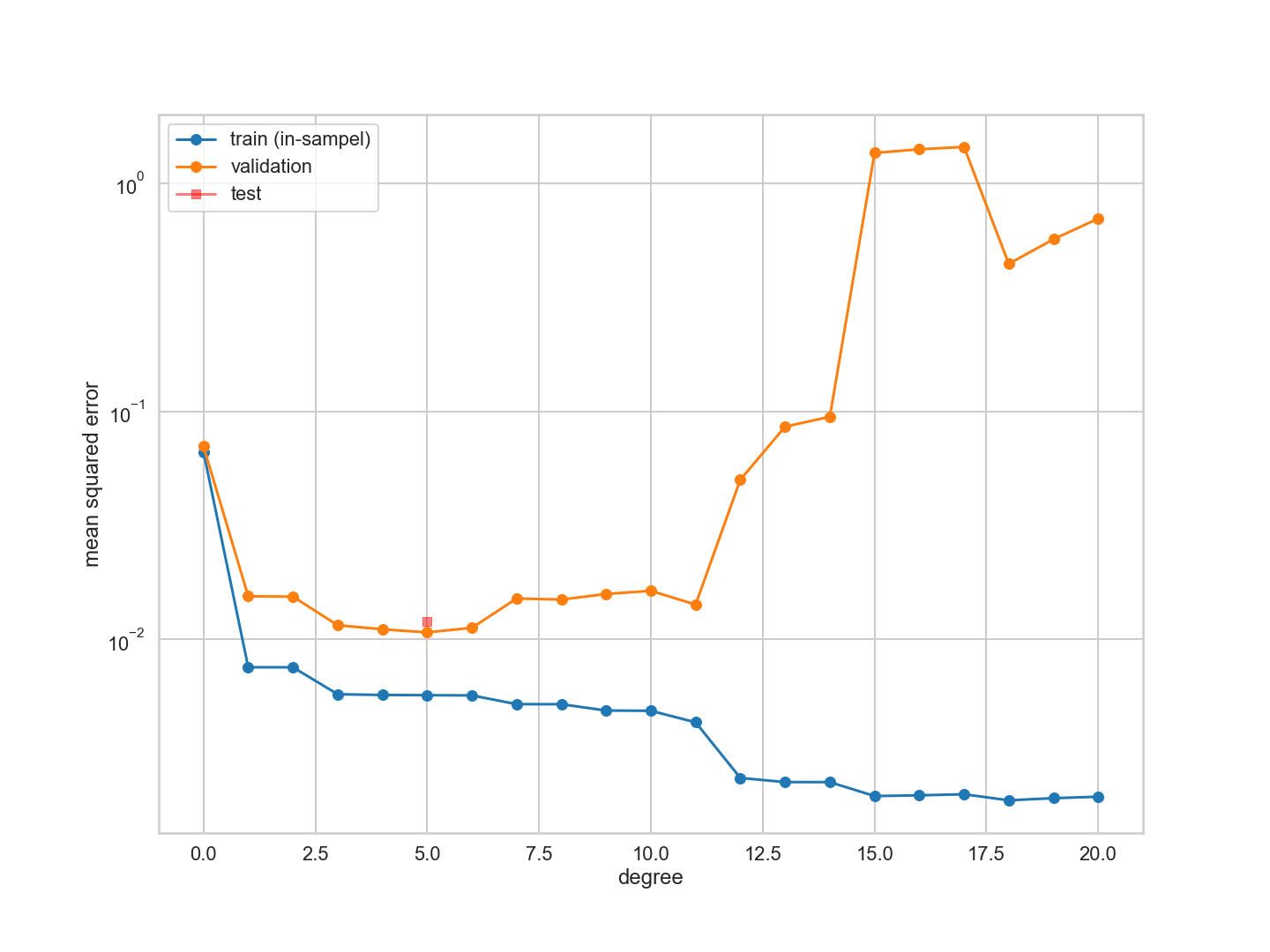
우리는 다항식 차수를 최소화하는 검증 세트를 얻었다.

다시 한번 교육 데이터와 검증 데이터 사이의 랜덤 분할을 선택한다 :

plt.figure(figsize=(20,15))
intrain, invalid = train_test_split(itrain, train_size=18, test_size=6)
xntrain = df.x[intrain].values
fntrain = df.f[intrain].values
yntrain = df.y[intrain].values
xnvalid = df.x[invalid].values
fnvalid = df.f[invalid].values
ynvalid = df.y[invalid].values

degrees = range(21)
error_train = np.empty(len(degrees))
error_valid = np.empty(len(degrees))
trainvalidlists = make_features(xntrain, xnvalid, degrees)

for d in degrees:
    Xntrain = trainvalidlists[d]['train']
    Xnvalid = trainvalidlists[d]['test']
    
    est = LinearRegression()
    est.fit(Xntrain, yntrain)
    
    error_train[d] = mean_squared_error(yntrain, est.predict(Xntrain))
    error_valid[d] = mean_squared_error(ynvalid, est.predict(Xnvalid))

mindeg = np.argmin(error_valid)
ttlist = make_features(xtrain, xtest, degrees)

clf = LinearRegression()
clf.fit(ttlist[mindeg]['train'], ytrain) 
pred = clf.predict(ttlist[mindeg]['test'])
err = mean_squared_error(ytest, pred)
plt.plot(degrees, error_train, marker='o', label='train (in-sampel)')
plt.plot(degrees, error_valid, marker='o', label='validation')
plt.plot([mindeg], [err], marker='s', markersize=10, label='test', alpha=0.5, color='r')

plt.ylabel('mean squared error')
plt.xlabel('degree')
plt.legend(loc='lower left')
plt.yscale('log')
print(mindeg)

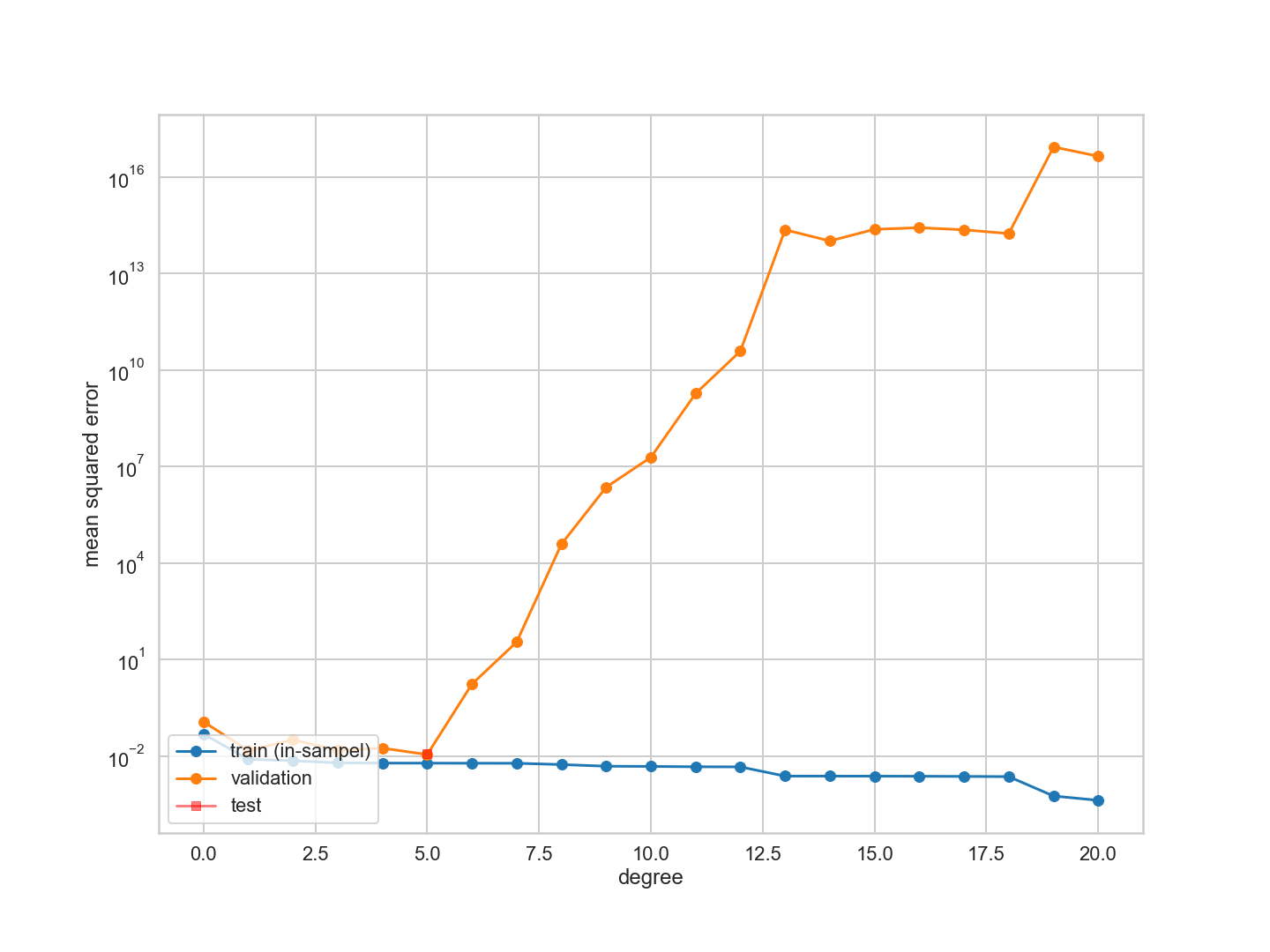
이번에는 다항식 차수를 최소화하는 유효성 검사 오류가 변경되었다.

Cross Validation

새로운 무작위 분할을 선택했기에 우리가 다항식 차수 또는 복잡도 $d$를 최소화하는 '최상의' 검증을 찾기 위해 그러한 무작위 분할을 여러 개 선택하고 이 과정보다 어떻게 해서든 평균을 내기를 원하게 만든다.

게다가 우리가 빠뜨린 검증 세트에는 두 가지 경쟁적인 요구가 있다. 집합이 클수록 표본 외 오차의 추정치가 더 좋다.

그러나 검증 세트가 작을수록 모델을 교육해야 할 데이터가 많아진다. 따라서 우리는 더 나은, 더 표현력 있는 모델을 적합시킬 수 있다.

우리는 이 두가지 바람의 균형을 맞추고, 또한, 이전 훈련 세트의 단일 train-validation split에서 무작위로 발생할 수 있는 어떤 특성에도 노출되지 않기를 원한다.

이를 처리하기 위해 복잡성 매개 변수 $d=a$(다항식 차수)를 갖는 주어진 가설 집합 $\cal{H}_a$에 대해 아래 그림에 설명된 교차 검증이라는 프로세스를 수행한다. 분할은 한 번이 아니라 여러 번 실시한다.

아래 그림에서 우리는 데이터 세트 $\cal{D}$의 훈련 세트 부분에서 4-folds를 생성한다. 즉, 세트를 대략 4등분한다는 의미이다. 아래 그림과 같이, 이것은 4가지 다른 방법으로 또는 접힐 수 있다. 각 fold마다 3개의 part에 대한 모델을 교육한다. 그렇게 훈련된 모델은 $g^-{Fi}$, 예를 들어 $g^-{F3}$로 명명된다. 위첨자 마이너스 부호는 축소 집합에 대해 교육 중임을 다시 한 번 나타낸다. $F3$ 모델이 세 번째로 교육되었음을 나타낸다. 각 fold마다 교육되는 모델은 다르다.

각 fold마다 모델을 교육한 후 나머지 한 유효성 검사 part에 대한 위험 또는 오류를 계산한다. 그런 다음 서로 다른 fold에서 검증 오류를 함께 추가하고 접힘 횟수로 나누어 평균 오차를 계산한다. 이 평균 오차는 다른 모델 $g^-_{Fi}$들에 대한 평균이다. 앞에서 설명한 유효성 검사 프로세스에서 $d=a$에 대한 유효성 검사 오차로 이 오류를 사용한다.

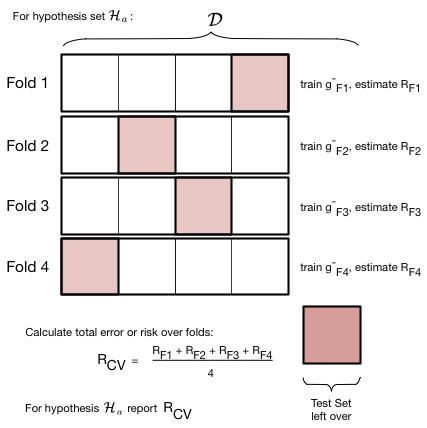
Fold 횟수는 데이터 분할 횟수와 같다. 예를 들어, 5개의 분할이 있다면 5개의 접힘이 있는 것이다. 교차 검증을 설명하려면 아래 적합치(평균 및 직선)를 사인 곡선에 대한 $\cal{H}_0$ 및 $\cal{H}_1$(데이터 점 3개만 있는 경우)를 고려해라.

The entire description of K-fold Cross-validation

우리는 앞으로 검증 집합 위험이 주어진 모델을 $d$의 함수로 선택하기 위해 사용한 방법으로 다항식 $d$ 차수에 대한 오차를 계산하기 위해 이 계획을 함께 적용했다.

1. training 데이터의 n_fold 파티션을 만든다.
2. 그런 다음 이 파티션의 n_fold - 1에 따라 훈련하고 나머지 parition에서 테스트 한다. 파티션(또는 folds)의 이러한 조합이 fold 되어 있으므로 fold risk가 있다.
3. 각 $d$, $R_{dCV}$의 값에 대해 그러한 모든 조합의 오류 또는 위험을 평균한다.
4. $d$의 다음 값으로 넘어가고, 3을 반복한다.
5. 그런 다음 위험 $d=*$를 최소화하는 d의 최적값을 찾아라.
6. 마지막으로 이 값을 사용하여 $\cal{H}_*$에 전체 이전 훈련 세트에 대한 최종 적합을 만든다.

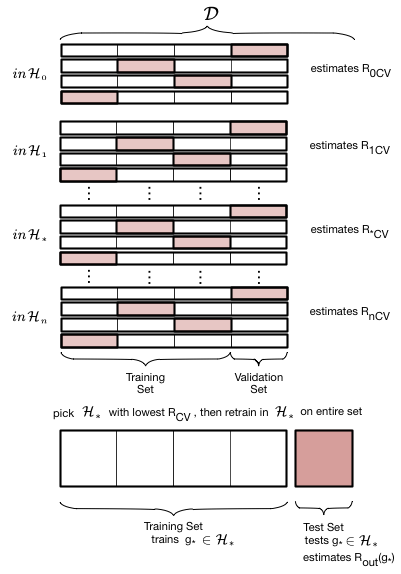
또한 교차 검증 오차가 표본 오류의 편향되지 않은 추정치라는 것을 보여줄 수 있다.

이제 Romney 투표 자료에 대한 4-fold 교차 검증을 실시하겠다. 우리는 복잡성을 0에서 20으로 증가시킨다. 각 경우에 우리는 이전 훈련 세트를 4번을 나누고 4번을 접고, 3번을 접은 다음 훈련시키고 유효성 검사 오류를 계산한다. 그런 다음 교차 검증 오류를 얻기 위해 4번 접은 부분의 오차를 평균하여 해당 $d$에 대한 교차 검증 오차를 구한다. 그리고 나서 우리는 전에 했던 것을 한다 : 교차 검증 오차가 가장 작은 가설 공간 $\cal{H}*$를 찾아내고 전체 훈련 세트를 사용하여 다시 적합시킨다. 그런 다음 시험 세트를 사용하여 $E{out}$을 추정할 수 있다.

from sklearn.model_selection import KFold

cv = KFold(n_splits=4)

n_folds=4
degrees=range(21)
results=[]

for d in degrees:
    hypothesisresults=[]
    for train, test in cv.split(itrain): # split data into train/test groups, 4 times
        tvlist=make_features(xtrain[train], xtrain[test], degrees)
        clf = LinearRegression()
        clf.fit(tvlist[d]['train'], ytrain[train]) # fit
        hypothesisresults.append(mean_squared_error(ytrain[test], clf.predict(tvlist[d]['test']))) # evaluate score function on held-out data
    results.append((np.mean(hypothesisresults), np.min(hypothesisresults), np.max(hypothesisresults))) # average

plt.figure(figsize=(20,15))
mindeg = np.argmin([r[0] for r in results])
ttlist=make_features(xtrain, xtest, degrees)
#fit on whole training set now.
clf = LinearRegression()
clf.fit(ttlist[mindeg]['train'], ytrain) # fit
pred = clf.predict(ttlist[mindeg]['test'])
err = mean_squared_error(pred, ytest)
errtr=mean_squared_error(ytrain, clf.predict(ttlist[mindeg]['train']))
errout=0.8*errtr+0.2*err
c0=sns.color_palette()[0]
#plt.errorbar(degrees, [r[0] for r in results], yerr=[r[1] for r in results], marker='o', label='CV error', alpha=0.5)
plt.plot(degrees, [r[0] for r in results], marker='o', label='CV error', alpha=0.9)
plt.fill_between(degrees, [r[1] for r in results], [r[2] for r in results], color=c0, alpha=0.2)
plt.plot([mindeg], [err], 'o',  label='test set error')
plt.plot([mindeg], [errout], 'o',  label='full sample error')


plt.ylabel('mean squared error')
plt.xlabel('degree')
plt.legend(loc='upper right')
plt.yscale("log")

교차 검증 오차는 낮은 차수로 최소화한 다음 증가한다는 것을 알 수 있다. 데이터 점이 너무 적기 때문에 접힘 오차 범위도 증가한다.