0. Intro

저번에 업로드했던 nlp-intro 시리즈는 자연어 처리에 대한 기법을 알기 쉽게 풀어서 설명할 예정입니다. 이번에는 또 다른 시리즈, 딥러닝을 이용한 자연어 처리입니다. 처음 기획할 때, 딥러닝의 화려하게 구현하는 것도 좋지만, 차근차근 원리를 정리하자!는 마음으로 시작했어요. 하지만 정리를 하다 보니 nlp-intro처럼 숫자 없이 마음 편하게 읽을 수는 없겠더라구요😭 최대한 쉽게 정리 해 보았습니다. 혹시 설명에 오류가 있거나 궁금한 점이 있으시면 언제든 연락 부탁드립니다🧐 (email: jung666597@cosadama.com)

1. 신경망 복습

1.1. 신경망의 추론

신경망은 쉽게 말해 함수입니다. 무언가를 입력하면, 다른 무언가가 출력됩니다. (단, 여기에 학습과 추론이라는 단계가 있습니다.)

입력층 -> 은닉층 -> 출력층 이렇게 이어지고,

Colored_neural_network

화살표에는 가중치weight가 존재해 기존 뉴런에 활성화함수h()를 적용한 값이 다음 뉴런의 값이 됩니다. 이때 이전 뉴런의 값에 영향을 받지 않는 편향bias가 더해집니다.

이렇게 인접하는 모든 층의 뉴런과 연결된 신경망을 완전연결계층fully connected layer라고 합니다.

은닉층의 첫번째 뉴런은 수식으로 다음과 같겠죠? 가중치의 합 + 편향이니까요.

$$ h_1 = x_1w_11 + x_2W_21 + b_1 $$

결국 모든 은닉층은 다음과 같이 정의될 수 있습니다. $$ (h_1, h_2, h_3, ... ,h_n) = (x_1, x_2)\begin{pmatrix} w_{11} & w_{12} & w_{13} & ... & w_{1n} \ w_{21} & w_{22} & w_{23} & ... & w_{2n} \end{pmatrix} + (b_1, b_2, b_3, ... ,b_4) $$

당연히 은닉층 뉴런들(h1, h2, h3, h4)는 (1,4)행렬이겠죠?

더 간단히 은닉층을 추상화 하면 다음과 같습니다.

$$ h = xW + b $$ - x: 입력

- h: 은닉층 뉴런

- W: 가중치

- b: 편향

import numpy as np



x = np.random.randn(10,2) # 입력



W1 = np.random.randn(2,4) # 가중치

b1 = np.random.randn(4)  # 편향



W2 = np.random.randn(4, 3) # 가중치

b2 = np.random.randn(3)  # 편향



h = np.matmul(x, W1) + b1

a = sigmoid(h)

s = np.matmul(a, W2) + b2

s

array([[-0.53493193, -0.5247171 , -2.64375572], [-0.54124544, -0.65299692, -2.89124709], [-0.72314367, 0.09814948, -1.14513823], [-0.43875181, -0.21611169, -1.98119464], [-0.74755378, 0.12793834, -1.18694412], [-0.65180853, -0.32071963, -2.22091246], [-0.54784024, -0.03119535, -1.68980056], [-0.45241895, -0.92681161, -3.30155571], [-0.38680553, -0.31997467, -2.12871497], [-0.73294214, 0.05678831, -1.09844678]])

미니배치

방금의 데이터x는 단일 데이터였습니다. 만약 이런 데이터가 몇 천만, 몇 조 개라면 어떨까요? 계산이 빠른 numpy array를 사용하더라도 계산하는데 시간이 오래걸릴 겁니다. 그래서 우리는 보통 mini-batch를 사용합니다. 즉, 데이터의 일부만 골라 학습하는 거죠. 그 일부가 미니배치mini-batch입니다. 예컨대 100만건의 데이터 중 100장을 임의로 뽑아 100장만 사용해 학습하는거죠.

???: 비선형 변환을 사용해야 한다구요?

앞서 보았던 은닉층(활성화 함수h())은 적용한 값이 그대로 이후 노드에 전해졌습니다. 이래선 그냥 곱하는 것과 크게 다를 바가 없습니다. h(x)=cx라면 3층 네트워크를 지난 순간 그냥 $c^3x$ 가 될겁니다. 즉, 신경망을 사용하는 이유가 줄어듭니다. 이때, 비선형인 활성화 함수를 사용해 실제 신경처럼 정보를 전달할지, 말지 정해줄 수 있습니다.

2. 선형, 비선형 개념 잡기

음..? 선형 함수, 비선형 함수가.. 뭐죠?

2.1. 선형결합Linear Combination

간단하게 선형 결합linear combination을 짚고 넘어가겠습니다. 벡터들의 선형결합은 쉽게 말해서 곱해서 다 더했을 때 $\sum$ 변하지 않은 것(벡터)의 집합을 의미합니다. 어렵죠? 조금 있다가 덧붙이겠습니다.

$(V,+,\times): 벡터공간$일 때, $$ \vec{v_1},\vec{v_2}, \cdots, \vec{v_n} \in V \And \alpha_n \in R, i = 1, 2, \cdots , n $$

$$ \sum_{k=1}^n \alpha_k\vec{v_k} = \alpha_1\vec{v_1}+\alpha_2\vec{v_2}+\cdots+ \alpha_n\vec{v_n}\in V $$

2.2. 유클리드 벡터 $V = R^n$

우리가 알던 벡터는 실제 세계의 벡터 즉, 크기와 방향을 갖는 물리적 의미의 유클리드 벡터입니다. 이때 벡터의 집합 $V = R^n$ 이고, 기본 연산(덧셈과 스칼라 곱)에 대해 닫혀 있습니다.

닫혀 있다의 의미는 $V = R^n$인 어떤 집합$V$에 대해 기본 연산(덧셈이나 스칼라 곱)을 했을 때 그 원소가 $\in R^n$라는 뜻입니다.

쉽게 말하자면 어떤 대상 집함에 덧셈, 스칼라 곱, 벡터나 행렬 곱을 했을 때, 그 원소가 원래 집합에 속한다는 의미입니다.

반대로 우리가 아는 행렬은 곱셈의 교환 법칙 $AB \neq BA$이 성립하지 않았습니다. 다르게 말하면 행렬은 곱셈에 대해서 열려 있습니다.

(행렬 곱이 교환되지 않는다는 명제는 (2,2) 행렬 두 개를 직접 곱 해보시면 알 수 있으실 겁니다.)

2.3. 벡터(부분) 공간

벡터 공간은 원소를 더하거나 스칼라 곱이 가능합니다. 즉, 교환법칙이 가능합니다.

벡터공간은 크기, 방향이 중요하지 않고, 기본연산(+, 스칼라 곱)이 성립해 다시 벡터 공간(기본연산 성립)에 속하는 벡터의 집합이기만 하면 성립하기 때문입니다.

즉, 벡터 공간은

두 원소를 더하거나, (덧셈)

주어진 원소를 임의의 실수 배만큼 자유롭게 늘리거나 줄인 대상이 (스칼라 곱 = 상수배)

다시 벡터 공간에 속하는 공간입니다.

수식으로 보면 다음과 같습니다. $$ \vec{v_1},\vec{v_2}, \cdots, \vec{v_n} \in V \And \alpha_n \in R, i = 1, 2, \cdots , n $$ 이며,

$(V,+,\times)$: 벡터 공간일 때

$S\subset V$ 이고, $(S,+,\times)$: 벡터공간 이라면

$S<V$: S는 V의 벡터공간(부분 공간)

입니다.

덧셈, 스칼라 곱에 대해서 닫혀있다면(기본연산이 닫혀있다면) 벡터공간(부분 공간)이라고 할 수 있습니다.

= $$ \begin{cases}

{}{}^{\forall}\vec{u},\vec{v} \in S \Rightarrow \vec{u}+\vec{u}\in S \ {}{}^{\forall}\vec{u} \in S, \alpha\in R \Rightarrow \alpha\vec{u} \in S \end{cases} $$ or $$ {}_{}^{\forall}\vec{u},\vec{v} \in S \And\alpha,\beta \in R\ \Rightarrow \alpha\vec{u}+\beta\vec{v}\in S $$

2.4. 벡터 공간을 만족하는 열 가지 공리

$V(\neq \varnothing)$인 집합이고,

$\vec{u}, \vec{v}, \vec{w} \in V \And \alpha,\beta\in R$ 이라고 합시다.

(1) 기본 연산의 닫힘성

덧셈: $\vec{u}+ \vec{v}\in V$

곱셈: $\alpha\vec{u}\in V$

(2) 덧셈 관련 공리

벡터 공간 V는 덧셈에 대해 닫혀 있습니다.(닫힘성closed under addition), 즉 a 및 b가 벡터 공간 V에 존재하면 a + b도 V에 존재해야 합니다.

덧셈의 교환 법칙: $\vec{u}+ \vec{v} = \vec{v}+\vec{u}$
덧셈의 결합 법칙: $(\vec{u}+\vec{v})+\vec{w} = \vec{u}+(\vec{v}+\vec{w})$
영 벡터가 존재(꼭 영벡터의 성분이 모두 0일 필요 없음. 덧셈에 대한 항등원이기만 하면 됨.): ${}{}^{\forall}\vec{u},{}{}^{\exists}\vec{0} \in V, \vec{u}+\vec{0}=\vec{u}$
덧셈 역원이 존재: ${}{}^{\forall}\vec{u},{}{}^{\exists}\vec{-u} \in V, \vec{u}+\vec{-u}=\vec{0}$

(3) 스칼라 관련 공리

벡터 공간 V는 스칼라 곱셈에 대해 닫혀 있습니다.(닫힘성closed under scalar multiplication), 즉 a가 V에 존재하고 α가 스칼라이면, αa도 V에 존재해야 합니다.

스칼라 곱의 결합 법칙: $\alpha(\beta\vec{u}) = \beta(\alpha\vec{u})$
~9.스칼라 곱의 분배 법칙:

- $\alpha(\vec{u}+\vec{v}) = \alpha\vec{u}+\alpha\vec{v}$

- $(\alpha+\beta)\vec{u} = \alpha\vec{u}+\beta\vec{u}$

스칼라 곱의 항등원: $1 \times \vec{u} = \vec{u}$

2.5. 더 자세한 선형결합Linear Combination

정의

$(V,+,\times)$: 벡터 공간일 때

$\vec{v_1},\vec{v_2}, \cdots, \vec{v_n} \in V \And \alpha_n \in R, i = 1, 2, \cdots , n$

$\sum_{k=1}^n \alpha_k\vec{v_k} = \alpha_1\vec{v_1}+\alpha_2\vec{v_2}+\cdots+ \alpha_n\vec{v_n}\in V$

$\vec{v}_n$은 V에 속해서 변하지 않습니다. (벗어나지 않습니다.)

오히려 $\alpha_n$은 어떤 실수R여도 되기 때문에 바뀔 수 있습니다.(값은 바뀔 수 있지만 벗어나지 않습니다.)

저러한 시그마가 가능하며, 변하지 않는 ${\vec{v_1},\vec{v_2}, \cdots, \vec{v_n}}$를 $vec{v_1}$부터 $\vec{v_n}$까지의 선형 결합이라고 합니다.

즉, 변하지 않는 $\vec{v_n}$에 어떤 스칼라를 곱해서 더해도 V에 속한다면, $V$의 원소 $\vec{v_n}$을 선형 결합이라고 합니다.

2.6. 딥러닝에서 벡터의 선형결합

생각보다 선형결합에 대한 설명이 길었군요. 미안합니다😅 본격적으로 왜 딥러닝에서 선형결합이 중요한지로 돌아가 봅시다.

$\alpha_n={a_1, a_2, \cdots, a_n\ }\in R$,

$S_n={v_1, v_2, \cdots, v_n\ }$까지 벡터일 때,

$\sum_{k=1}^n \alpha_kS_k=c_1v_1 + c_1v_1 + \cdots + c_nv_n $ 입니다.

즉, 벡터끼리의 곱셈이 아니라 벡터의 각 원소에 상수배를 한 것을 의미합니다.

$$ A = \begin{bmatrix}x_{1,1} & x_{1,2} & x_{1,3} \ \end{bmatrix},

B = \begin{bmatrix} a\ b\ c \end{bmatrix} $$ 변수를 원소로 갖는 행벡터 A와 상수 열벡터 B가 있다고 할 때, 이 둘을 곱해서 더한 것 즉,

$$ ax_{1,1} + bx_{1,2} + cx_{1,3} $$ 위 식의 A는 선형 결합입니다.

A는 (1,3), B는 (3,1)벡터입니다. A의 열의 차수와 B의 행의 차수가 같기 때문에 곱셈이 가능합니다.

따라서, A는 선형결합입니다.

앞에서 언급했듯이, 이런 경우에는 이전 노드의 값 $\times$가중치와 상수항의 합이 그대로 전달됩니다.

2.7. 선형함수

만약 A가 벡터의 집합인 행렬이라면

$$ A = \begin{bmatrix}x_{1,1} & x_{1,2} & x_{1,3} \ x_{2,1} & x_{2,2} & x_{2,3}\ \vdots & \vdots & \vdots \end{bmatrix},

B = \begin{bmatrix} a\ b\ c \end{bmatrix} $$

$AB$는 다음과 같이 표현되고

$$ AB=\begin{cases} ax_{1,1} + bx_{1,2} + cx_{1,3} = y_1 \ ax_{2,1} + bx_{2,2} + cx_{2,3} = y_2\ ax_{3,1} + bx_{3,2} + cx_{3,3} = y_3\ \vdots \end{cases} $$

연립방정식(함수function) 으로는 이렇게 표현됩니다.

이때, 우리에게 주어진 데이터는. $x_n, y_n$입니다.

linear_regression

그래프를 봅시다. 우리에게 주어진 데이터는 저 파란 점들입니다. x값과 y값을 갖는 점들이 어떤 식으로 분포 되어있는지 회귀regression(독립변수가 종속변수에 얼마나 영향을 미치는지 분석. 최소한으로 떨어진 선을 긋는다고 생각하면 됩니다.)을 사용해 분석한다고 합시다.

우리에게 주어진 데이터는 점들의 $x_n$과 $y_n$값들입니다. x와 y를 구하는 것이 익숙하지만, 회귀선(함수)을 그리려면 행렬 B의 a, b, c값들을 구해야 합니다. a,b,c는 계수(변수에 곱해진 것-파라미터) 입니다.

선형대수, 혹은 회귀에서 선형linear이냐는 물음은

변수와 파라미터가 선형인지를 묻는 겁니다.

이때 우리에게 주어지는 정보는 x, y 값입니다. 예컨데 회귀를 통해 예측한 식이 $ax^2+bx+c=y$ 꼴이라고 합시다. 데이터가 무수히 많이 주어지거나, x, y값을 여러 개로 잘라서 분석한다면 우리는 해당하는 식들을 행렬의 곱으로 표현할 수 있습니다.

$$ AB= \begin{bmatrix}x_{1}^2 & x_{1} & 1 \ x_{2}^2 & x_{2} & 1\ \vdots & \vdots & \vdots \end{bmatrix}

\begin{bmatrix} a\ b\ c \end{bmatrix}

\begin{bmatrix} y_1\ y_2\ y_3\ \vdots \end{bmatrix} $$

선형 결합인 AB에 대해 우리가 구해야 할 것은 a, b, c입니다. (a, b, c는 연립방정식에서 계수고, 회귀식에서는 파라미터입니다.) 결국 우리는 주어진 변수 $x_n, y_n$와 계수 a, b, c가 선형으로 결합되어 있는지를 질문 받고 있네요. (결국 행렬의 곱이 성립하냐는 질문과 같습니다.)

딥러닝에서 선형성을 생각해 보면 계수 즉, 노드와 가중치가 선형 결합의 관계에 있을 때 선형모델입니다.

dl_linear

dl_linear_eg1

출처: https://www.youtube.com/watch?v=umiqnfQxlac&t=133s

가중치가 없을 때도 선형이고,

각 노드에 가중치가 곱해져서 더해진 것도 선형입니다.

노드 값에 제곱이나 로그를 취한 것에 가중치가 차례차례 전부 곱해져 더한다면 이 또한 선형입니다.

이전 노드x(logx)와 결과y가 벡터 공간에 있기 때문입니다.

2.8. 비선형 함수, 비선형 모델

그렇다면 비선형 모델은 무엇일까요?

dl_non_linear

출처: https://www.youtube.com/watch?v=umiqnfQxlac&t=133s

차차 설명하겠지만 시그모이드 함수를 통한 z값은 $z = \frac{1}{1+e^{-y}}$입니다. 이때 방금 선형으로 계산한 $y=w_1x_1 +w_2x_2 + \cdots +w_nx_n$입니다. 따라서 z는 위와 같은 꼴이 나옵니다.

선형함수는 곱해서 더한 값이 그대로 다음 층의 노드에 그대로 적용되었습니다. 하지만 비선형함수에서는 선형으로 계산된 값을 시그모이드 함수, reLU함수 등에 적용해 변환된 값을 다음 노드에 적용합니다. 이 역할을 하는 함수를 보통 $h(x)$로 표현합니다.

2.9. 정리

선형함수:

- 꼭 1차 함수 아님! 곡선 가능. 직선일 필요 없음.

- 변수 계수가 선형 관계인 경우(행렬을 곱셈이 가능한 경우)

- 다음 층의 노드 $y=w_1x_1 +w_2x_2 + \cdots +w_nx_n$

비선형 함수:

- 다음 노드의 값h(y)=z이 변수variable와 계수coefficient의 선형 관계가 아닌 경우.

- 선형 함수로 계산된 값이 그대로 다음 노드에 적용되는 것이 아니고!

- 다시 활성화 함수 h(x)에 적용해 조건에 따라 다르게 계산된(conditional하게 나온) 값이 다음 노드에 적용되는 경우.

라고 할 수도 있겠군요.

출처: https://www.youtube.com/watch?v=umiqnfQxlac&t=133s

3. 비선형 함수

3.1. 활성화 함수에서 비선형 함수가 중요한 이유

선형 함수(y=ax+b)를 활성화 함수로 사용하면 신경망의 층수를 깊게 하는 의미가 옅어집니다.

만약 h(x)=ax+b인 상태로 3층의 신경망 y(x)을 만든다면

$$h(x) = ax$$

$$y(x) = h(h(h(x))) = a^{3}x$$

이렇게 은닉층을 만들어서 가중치를 주는 의미가 줄어듭니다. 따라서 신경망을 만들 때 비선형 함수를 사용하도록 합시다.

(다음 nlp-intro 포스팅에서 왜 nlp에서 딥러닝을 사용하는지에 대해 차차 설명 드리겠습니다.)

3.2. 비선형 함수의 종류

대표적인 비선형 함수는 계단 함수와 시그모이드 함수, Relu함수가 있습니다.

비선형 함수의 종류

계단 함수
시그모이드 함수
ReLU함수

계단 함수

계단함수는 퍼셉트론에서처럼 특정 범위 마다 값을 정해주는 형태입니다.

파이썬으로 표현하면 다음과 같습니다.

def step_function(x):
    if x>0:
        return 1
    else:
        return 0

stair_function

출처: https://snowdeer.github.io/machine-learning/2018/01/04/activation-function/

시그모이드 함수

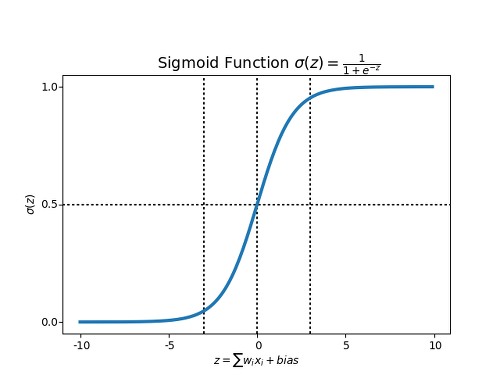
시그모이드 함수는 다음과 같습니다.

$$ h(x) = \frac{1}{1+exp(-x)} $$

exp(-x )는 자연상수 e의 -x제곱입니다.

겁 먹을 필요 없습니다. 어차피 컴퓨터가 계산해 줄 겁니다.

$$ exp(-x ) = e^{-x} $$

파이썬으로 구현하면 이런 식이 되겠군요.

import numpy as np
import matplotlib.pyplot as plt

  
def step_function(x):
    return np.array(x>0, *dtype*=np.int)

x = np.array([-5.0, 5.0, 0.1])
step_function(x)
plot(x,y)
plt.ylim(-0.1,1.1)  # y축 범위 지정
plt.show()

sigmoid

출처: https://snowdeer.github.io/machine-learning/2018/01/04/activation-function/

계단 함수는 값이 뚝뚝 끊기는 반면,

시그모이드 함수는 입력에 따라 값이 연속적(실수)으로 변화합니다.

참고: 로지스틱함수는 음의 무한대부터 양의 무한대까지의 실수값을 0부터 1사이의 실수값으로 1 대 1 대응시키는 시그모이드 함수입니다. 로지스틱 회귀는 시그모이드 함수가 주는 비선형적 특성을 이용해 어느 정도 크기 이상이면 1, 이하면 0으로 이진 분류하는데 사용됩니다.

참고: 데이터 사이언스 스쿨

ReLU함수

정의: 입력이 0을 넘으면 그 입력을 그대로 출력하고 0 이하이면 0을 출력하는 함수

$$ h(x)= \begin{cases} x (x>0) \ 0 (\leq 0) \end{cases} $$

def relu():
    return np.maximum(0,x)

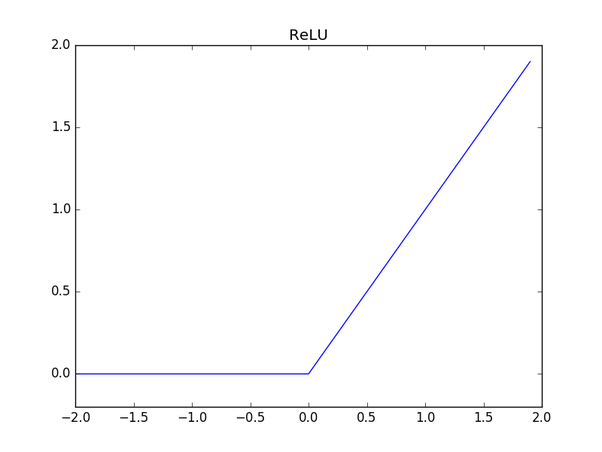
relu_function

(np.maximum은 두 입력 중 큰 값을 선택해 반환하는 함수입니다.)

sigmoid_output

4. 마무리

여기까지가 딥러닝을 이용한 자연어 처리 첫 포스팅이었습니다. 굉장히 원론적이고 지루하게 보일 수 있는 (수학이 낭낭한) 글이었네요. 하지만 저는 많은 사람들이 선형, 비선형 같이 자잘한 개념들도 잘 소화할 수 있으면 좋겠어요. 그래야 학습할 때나, 실전 한가운데서 당황하지 않을 수 있다고 믿기 때문이죠. 우리는 한 번도 가보지 않은 길을 가고 있으니까 지도의 표기법 정도는 알아 놓아야 길을 찾을 수 있지 않을까요? 차근차근 같이 공부하다 보면 딥러닝도, 자연어 처리도 어느새 이해하고, 프로젝트도 설계할 수 있을 겁니다.

최대한 쉽게 설명한다고 애를 써 봤는데 어떠셨나요? 만약 수식이나 행렬 등이 헷갈리거나 의미를 잘 모르시겠다면 딥러닝을 위한 선형대수학 같은 키워드로 검색하시면 더듬더듬이라도 알아가실 수 있을 거예요. 백신 여파로 생각보다 블로그 글을 많이 소화하지 못했네요. 지금 하고 있는 프로젝트도 대강 마무리 되고 있으니 11, 12월에는 더 바짝 글을 써 보도록 하겠습니다.😋

그럼 다음 글에서 만나요🧐

딥러닝을 이용한 자연어 처리-1

0. Intro

1. 신경망 복습

1.1. 신경망의 추론

미니배치

???: 비선형 변환을 사용해야 한다구요?

2. 선형, 비선형 개념 잡기

2.1. 선형결합Linear Combination

2.2. 유클리드 벡터 $V = R^n$

2.3. 벡터(부분) 공간

2.4. 벡터 공간을 만족하는 열 가지 공리

2.5. 더 자세한 선형결합Linear Combination

2.6. 딥러닝에서 벡터의 선형결합

2.7. 선형함수

\begin{bmatrix} a\ b\ c \end{bmatrix}

2.8. 비선형 함수, 비선형 모델

2.9. 정리

3. 비선형 함수

3.1. 활성화 함수에서 비선형 함수가 중요한 이유

3.2. 비선형 함수의 종류

4. 마무리